Один из основателей математической логики и теории множеств

К 160–летию со дня рождения Джузеппе Пеано

Джузеппе Пеано (Giuseppe Реаnо) родился 27 августа 1858 г в городе Кунео (Северная Италия). По окончанию лицея, поступил в Туринский университет в 1876 году, который окончил в 1880 году с отличием. В 1890-1932 годах работал профессором этого университета. Профессор Военной академии (1887—1901). Член Туринской Академии наук.

Пеано исследовал вопросы о возможно более широких условиях существования решений дифференциальных уравнений, определение понятия кривой и др. Занимался вопросами обоснования математики.

Пеано и его ученики Амодео, Фано, Пиери, следуя идеям Г.В.Лейбница, изложили математику в точной символической форме, без слов. Написанный им в 1895-1908 годах пятитомник "Формуляр математики"- энциклопедия, в которой разделы математики и логики излагаются на разработанном им символическом языке в виде формальной системы.

В линейной алгебре он первым дал аксиоматическое определение n-мерного линейного пространства (1888). Важный вклад Пеано внёс в арифметику, создав в 1891 году систему аксиом натурального ряда чисел, которая теперь называется системой аксиом Пеано.

Необходимость формализации арифметики не принималась всерьёз до появления работы Германа Грассмана, который показал в 1860-х, что многие факты в арифметике могут быть установлены из более элементарных фактов о функции следования и математической индукции. В 1881 году Чарльз Сандерс Пирс опубликовал свою аксиоматизацию арифметики натуральных чисел. Формальное определение натуральных чисел в 1889 году сформулировал итальянский математик Пеано, основываясь на более ранних построениях Грассмана, в своей книге «Основания арифметики, изложенные новым способом» (лат. Arithmetices principia, nova methodo exposita). В 1888 году (за год до Пеано) практически в точности подобную аксиоматическую систему опубликовал Дедекинд. Натуральные числа возникли естественным образом, возможно, еще в доисторические времена при счёте предметов, потому и «натуральные», что ими обозначались реальные неделимые объекты. Во времена Пифагора, в процессе философского осмысления и переосмысления исходного предметного содержания, арифметическое понятие числа подверглось глубокой теоретической переработке.

Философская переработка натурального числа выразилась в том, что оно было универсализировано как всеобщее понятие, оно было абсолютизировано как основа всего сущего и оно стало трактоваться не как внешняя, а как внутренняя характеристика всех вещей и явлений.

Каждый школьник слышал такое понятие, как аксиома. Аксиома – это утверждение, не требующее доказательства. В математике это понятие играет очень важную роль. Вся математика опирается на аксиомы, из которых потом последовательно выводятся (доказываются) все остальные математические утверждения (это и теоремы, которые мы учим в школе и различные формулы).

Полный список аксиом геометрии довольно длинный и поэтому в деталях не изучается, и упоминаются лишь те аксиомы, которые необходимы с точки зрения методики обучения математике. А как обстоит дело с аксиомами арифметики? У многих с арифметикой ассоциируется прежде всего таблица умножения, но вряд ли кто-нибудь когда-нибудь доказывал в школьном курсе её правильность. Можно даже задать такой вопрос: «Почему для натуральных чисел справедливы законы арифметических действий?» Так уж традиционно повелось, что в школе не говорят о том, что арифметика тоже может быть построена на основе аксиом, подобно тому, как это делается в геометрии.

Почему же, имея перед собой выдающийся образец дедуктивного изложения геометрии, воплощенный ещё в «Началах» Евклида, в котором, несмотря на все недостатки, математики примерно до конца XVIII века видели идеал математической строгости, они не предприняли попыток логически обосновать арифметику?

Во-первых, фундаментальная причина связана с гносеологической проблемой обоснования математики. Вместо того чтобы, начав с целых и рациональных чисел, перейти к иррациональным и комплексным числам, а затем к алгебре и математическому анализу, так уж исторически сложилось, что события в последовательном обосновании математики развивались в обратном порядке. После доказательства в начале прошлого века теорем Гёделя о неполноте стало понятно, что всё это было вовсе не случайно.

Во-вторых, можно указать и на то, что до второй половины XIX века обоснование основных утверждений и алгоритмов арифметики натуральных чисел, а также правил арифметических действий можно было осуществить без её аксиоматизации.

Математическая строгость характеризует доказательство с его формальной стороны, с точки зрения корректности определений, полноты посылок и независимости принятых аксиом. Значительную роль в достижении математической строгости «основных законов арифметики» сыграл как раз Джузеппе Пеано.

Занимаясь преподаванием математики, Пеано обнаружил недостаточность математической строгости существовавших тогда арифметических доказательств, требующих усовершенствования оснований математики.

Мы привыкли со школьных лет пользоваться привычными математическими обозначениями и нотациями. И нам кажется что так было если не "всегда", то очень и очень долго. Однако же нет! Вплоть до конца XIX века, к примеру, арифметика не была формализована (что уж говорить про другие разделы математики!). Только на рубеже девятнадцатого и двадцатого веков Джузеппе Пеано предложил систему аксиом, определяющих натуральный ряд. Только с помощью аксиом Пеано стало возможным формализовать арифметику. И только после их введения у математиков появился инструмент для доказательства основных свойств натуральных и целых чисел, а также возможность использовать целые числа для построения чисел рациональных и вещественных (действительных).

Аксиомы Пеано являются исторически первой из систем аксиом для натуральных чисел. Аксиомы Пеано позволили формализовать арифметику. После введения аксиом стали возможны доказательства многих свойств натуральных и целых чисел, а также использование целых чисел для построения формальных теорий рациональных и вещественных чисел.

В аксиоматике Пеано первоначальные понятия: множество натуральных чисел (обозначается N), единица (обозначается 1), следующее число (следующее для числа n обозначается n'). Пеано определил натуральный ряд чисел следующими пятью аксиомами:

1. В N существует натуральное число 1, называемое единицей.

2. За каждым натуральным числом n непосредственно следует однозначно определенное натуральное число n', называемое следующее за n.

3. Единица, т.е. натуральное число 1, непосредственно не следует ни за каким натуральным числом.

4. Каждое натуральное число непосредственно следует не более чем за одним натуральным числом.

5. Любое подмножество М из множества N, содержащее единицу, и вместе с каждым числом из М, содержащее следующее за ним число, совпадает с множеством N.

Эти аксиомы оказались проще, чем аксиомы геометрии. Просто поразительно, что на такой, казалось бы, довольно скудной на первый взгляд основе можно построить всю арифметику. А именно определить сложение, умножение и другие арифметические действия над числами, ввести отрицательные, рациональные и иррациональные числа и основные правила действий с ними, хотя это может быть математически строго сделано не так скоро.

В аксиоматике Пеано содержится вся арифметика, потенциально расширяющаяся на бесконечное множество случаев, подчиняющихся арифметическим правилам, опирается на следующее убеждение математиков. Числа для них являются самостоятельными идеальными объектами и на всех уровнях математики составляют определенную иерархию строгости, основанную на степени глубины проникновения в их свойства.

Непротиворечивость арифметики Пеано доказана в 1936 году Генценом с помощью трансфинитной индукции. Как следует из второй теоремы Гёделя о неполноте, это доказательство не может быть проведено средствами самой арифметики Пеано.

Оценивая усилия, потраченные в первые десятилетия XX века на аксиоматику, выдающийся немецкий математик и философ математики Герман Вейль в сборнике работ «О философии математики» написал: "В системе математики имеются два обнаженных пункта, в которых она, может быть, соприкасается со сферой непостижимого. Это именно принцип построения ряда натуральных чисел и понятие континуума."

Пеано определил также операции сложения и умножения на множестве натуральных чисел.

Операция сложения по Пеано – это такая операция «+», которая обладает следующими свойствами:

6. n + 1 = n’;

7. n + m’ = (n + m)’;

Операция умножения по Пеано – это такая операция « ∙ », которая обладает следующими свойствами:

8. n ∙ 1 = n;

9. n ∙ m’ = n ∙ m + n.

Для операции сложения также выполняются следующие свойства:

1. (n + m) + k = n + (m + k) для любых натуральных чисел n, m, k (это свойство называется ассоциативность);

2. n + m = m + n для любых натуральных чисел n, m (это свойство называется коммутативность).

Аналогичные свойства выполняются и для умножения:

1. (n ∙ m) ∙ k = n ∙ (m ∙ k) для любых натуральных чисел n, m, k (ассоциативность);

2. n ∙ m = m ∙ n для любых натуральных чисел n, m (коммутативность);

И, наконец, свойство, которое связывает операции сложения и умножения:

n ∙ (m + k) = n ∙ m + n ∙ k для любых натуральных чисел n, m, k (это свойство называется дистрибутивность).

Таким образом, благодаря Пеано, мы получили все, что нам необходимо для работы с натуральными числами.

Ряд натуральных чисел – довольно тонкая структура математики, которая гораздо сложнее, чем большинство других первичных понятий, хотя оно и является простейшим математическим понятием.

Как следует из теоремы Гёделя о неполноте, существуют утверждения о натуральных числах, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом Пеано.

Моррис Клайн, историк математики, пошутил: «Как бы то ни было, в 90-е годы XIX в., через каких-нибудь шесть тысяч лет (!) после того, как египтяне и вавилоняне “пустили в оборот” целые числа, дроби и иррациональные числа, математики смогли наконец доказать, что 2+2 = 4».

Давайте же докажем, что 2 + 2 = 4 и 2 ∙ 2 = 4.

Пример 1. Доказать, что 2 + 2 = 4.

Доказательство.

Используем аксиоматику Пеано и получим:

2 + 2 = 2 + 1’ = (2 + 1)’ = (2’)’ = 3’ = 4.

Пример 2. Доказать, что 2 ∙ 2 = 4.

Доказательство. Используем аксиоматику Пеано и получим:

2 ∙ 2 = 2 ∙ 1’ = 2 ∙ 1 + 2 = 2 + 2.

А в предыдущем примере мы уже доказали, что 2 + 2 = 4. Таким образом, можем заключить, что 2 ∙ 2 равно 4.

В геометрии Пеано установил основы, на которых можно осуществить логическое построение геометрий Евклида (1889). Он первый построил непрерывную (жорданову) кривую, которая полностью заполняет квадрат ("кривая Пеано").

Пеано — один из создателей современной математической логики. Его логическая теория занимает промежуточное положение между алгебраическими системами Ч. Пирса и Э. Шрёдера, с одной стороны, и функциональным подходом Г. Фреге и П. Рассела, с другой. Пеано принадлежит одна из первых дедуктивных систем логик высказываний (1891).

Пеано провёл различие между отношением включения класса в класс (⊂) и отношением принадлежности элемента к классу ∈, между единичным классом и единственным элементом этого класса, а также внёс вклад в разработку теории определений через абстракцию (введя, в частности, понятие образования класса через абстракцию). Логические идеи Пеано послужили переходным звеном в цепи исторического развития от старой алгебры логики (в той форме, какую ей придали работы Буля, Джевонса, Порецкого, Э. Шрёдера и др.) к современной форме математической логики.

Разработанная им оригинальная логическая символика впоследствии стала общеупотребительной.

В 1887 году Пеано ввёл очень общее понятие векторнозначных функций точечных множеств и определил для них понятие производной и интеграла, которые при соответствующих уточнениях могут рассматриваться теперь как понятие производной одной функции множества по другой и интеграла Лебега – Стилтьеса.

Известно, что Пеано серьёзно интересовался философией, например, в 1900 году он участвовал в Международном философском конгрессе в Париже. Даже чисто математические работы Пеано всегда были посвящены принципиальным философским проблемам, что шло вразрез со стремлением к специализации научного знания, характерным для того времени.

Пеано также создал международную искусственный язык Latina sine flexione (латино сине флексионе), который был упрощенной форме латыни, над которым работал в 1903–1904 годах. Он был президентом Академии международных искусственных языков.

Умер Джузеппе Пеано 20 апреля 1932 года от сердечного приступа в городе Турине.

Джузеппе Пеано – автор более 200 книг и статей. Именем Пеано назван один из астероидов. Его имя носят следующие математические объекты: кривая Пеано; производная Пеано; арифметика Пеано; формула Тейлора – Пеано.

• Первый конгресс был проведён в Цюрихе с 9 по 11 августа 1897 года, по инициативе Георга Кантора, основателя и первого президента Германского математического общества. В оргкомитет Конгресса входили Феликс Клейн, А. А. Марков, Анри Пуанкаре. Всего участников было 208, из них 12 — из России. На I конгрессе выступали сам Кантор, Адамар, Пикар, Гурвиц, Вольтерра, Пеано и другие известные математики. Пуанкаре приехать не смог, но прислал свой доклад «Об отношениях между чистым анализом и математической физикой». Заключительный доклад Клейн посвятил проблемам реформы математического образования.

• Лати́но-си́не-флексио́не (Latino sine flexione — латынь без словоизменения) — международный искусственный язык на основе латинского языка, созданный Джузеппе Пеано в 1903 году. После доработки в 1908 году стал называться интерлингва (не следует путать с другим искусственным языком с аналогичным названием).

• Уже в 1890 году внимание Уайтхеда привлёк один из самых его многообещающих учеников в Кэмбридже — Бертран Рассел. В июле 1900 года они отправились в Париж на Первый международный конгресс по философии, где их поразило выступление Джузеппе Пеано и в особенности аксиомы Пеано: принципы арифметики, казалось, можно было свести к началам символической логики. Рассел не только освоил аксиомы Пеано, но и значительно обобщил его идеи в своём первом наброске «Принципов математики» (1900). Ознакомившись с этой работой, Уайтхед признал, что логика — более фундаментальная дисциплина, чем математика, и что вся математика строится на «уточнённых» началах формальной логики.

• В 1899 году Д. Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.

• Чем же особенно знаменит Пеано?

Во-первых, он впервые аксиоматизировал множество натуральных чисел. Грубо говоря, до Пеано слова "множество натуральных чисел" использовали интуитивно, а не строго математически. Что уж говорить о других числах?

Система аксиом Пеано достаточно простая и логичная. Она включает пять аксиом, из которых выводятся все свойства натуральных чисел: 1 является натуральным числом; число, следующее за натуральным, также является натуральным; 1 не следует ни за каким натуральным числом; если натуральное число a непосредственно следует как за числом b, так и за числом c, то b и c тождественны; аксиома индукции: если какое-либо предложение доказано для 1(база индукции) и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа (шаг индукции), то это предложение верно для всех натуральных чисел. Понятно, что в множестве натуральных чисел (как мы его представляем интуитивно) эти аксиомы обязательно выполнены.

Интересно другое. Оказывается, что если у вас есть непротиворечивая система аксиом, более богатая, чем аксиоматика Пеано, то обязательно существует утверждение, которое вы не можете ни доказать, ни опровергнуть в этой системе аксиом! (Этот факт называется Теорема Гёделя о неполноте.)

Иными словами, как бы вы ни аксиоматизировали множество натуральных чисел, всегда будет утверждение про натуральные числа, которое нельзя ни доказать, ни опровергнуть!

Во-вторых, это остаточный член "в форме Пеано" для ряда Тейлора. За что Пеано знают все первокурсники.

В-третьих, это кривая Пеано. Такая замечательная кривая, которая через каждую точку квадрата проходит ровно один раз. В частности, тем самым показывает, что множества [0;1] и [0;1]2 равномощны. А еще показывает, что у двух равномощных множеств может быть разная площадь.

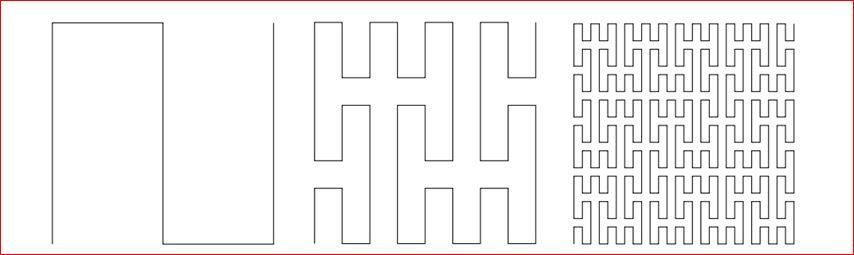
Кривая строится итеративно (кривая-фрактал), вот первые три итерации ее построения.

• Шольцем написана компактная «История логики» (1931, переиздана в 1959 как «Очерк истории логики»), где история предмета трактуется с предельно формалистических позиций. По Шольцу, логика становится строгой дисциплиной благодаря работам Лейбница, Ламберта, де Моргана, Буля, Э. Шрёдера, Пеано, Фреге, Рассела. Формальная логика оправдана в той мере, в которой она может быть представлена как символическая. Всё содержание логики, которое не охватывается разработанными этой линией логиков исчислениями, должно быть выведено за её пределы в области психологии или методологии науки.