ОТЕЦ БУКВЕННОЙ АЛГЕБРЫ

Франсуа Виет всегда упоминается как один из самых выдающихся учёных всех времен. Его имя вполне заслужено ставится в один ряд с такими личностями как Пифагор, Евклид, Вильгельм Лейбниц, Рене Декарт.

На то, какой мы в наше время видим алгебру, больше всего повлиял именно этот человек.

Франсуа Виет, сеньор де ля Биготьер — французский математик, основоположник символической алгебры. Свои труды подписывал латинизированным именем «Франциск Виета» (Franciscus Vieta), поэтому иногда его называют «Виета». По образованию и основной профессии — юрист.

Франсуа Виет родился в 1540г. в Фонтене-ле-Конт, что в 60 километрах от знаменитой крепости гугенотов ла-Рошель. Его отец был прокурором, а мать, Маргарита Дюпон, происходила из знатной семьи и имела хорошие связи с правящими кругами Франции, что облегчило дальнейшую карьеру её сына.

Франсуа учился сначала в местном францисканском монастыре, а затем — в университете Пуатье, где получил степень бакалавра (1560).

С 19 лет он работал адвокатом. Как адвокат Виет пользовался у населения авторитетом и уважением. Он был широко образованным человеком. Знал астрономию и математику и все свободное время отдавал этим наукам. Но уже через четыре года поступил на должность секретаря к знатному дворянину-гугеноту де Партене (Гугеноты - последователи кальвинизма, одного из основных течений Реформации Церкви).

Одновременно он стал у него домашним учителем, занимаясь космогонией с его 12-летней дочерью Екатериной. В это время он сам увлёкся изучением тригонометрии и астрономии. Преподавая астрономию, Виет пришел к мысли составить труд, посвященный усовершенствованию птолемеевской системы. Затем он приступил к разработке тригонометрии и приложению её к решению алгебраических уравнений.

По-видимому, в это время он вывел формулы для синусов и косинусов кратных углов, т.е. формулы для sin(mx) и cos(mx), дающие разложения по степеням sinx и cosx. При составлении обширных таблиц тригонометрических функций Виет с большим искусством применил десятичные дроби. Глубокий интерес к тригонометрии у него был вызван желанием сделать астрономию более точной.

Франсуа Виет сам не считал себя математиком. Он говорил, что занимается математикой в свободное время для собственного удовольствия. При этом, будучи состоятельным человеком, свои труды он за свой счет издавал и рассылал ученым во все уголки Европы. В историю Франсуа Виет вошел как выдающийся математик, автор многих эпохальных научных открытий.

После смерти де Партене и замужества Екатерины Виет последовал за своей ученицей в Париж. Он занимался правом, оказывал юридические и судебные услуги. В Париже ему было легче узнать о достижениях ведущих математиков Европы. С некоторыми учёными Виет познакомился лично. Так, он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вёл дружескую переписку.

Благодаря своему таланту и отчасти благодаря браку своей бывшей ученицы с принцем де Роганом, Виет сделал блестящую карьеру. Говорят, что его клиентами были королева Англии Мария и Элеонора Австрийская. В 1571 году он стал советником парламента, а вскоре стал тайным советником короля Генриха III, а после его убийства в 1589 году, он до 1602 года служил Генриху ΙV.

В ночь на 24 августа 1572 года в Париже произошла Варфоломеевская ночь. В ту ночь вместе со многими гугенотами погибли муж Екатерины де Партене и математик Рамус. Во Франции началась гражданская война. Через несколько лет Екатерина де Партене снова вышла замуж. На сей раз её избранником стал один из видных руководителей гугенотов — принц де Роган. По его ходатайству в 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать от имени короля выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.

Это позволило ученому позабыть о материальных трудностях, но также и привело к возникновению у Виета врагов. Так, один из влиятельных домов Франции, настроенных против советника, добился устранения его от занимаемой должности.

Но главной страстью Виета была математика. Он глубоко изучил сочинения классиков Архимеда и Диофанта, ближайших предшественников Кардано, Бомбелли, Стевина и других. Виета они не только восхищали, в них он видел большой изъян, заключающийся в трудности понимания из-за словесной символики.

Почти все действия и знаки записывались словами, не было намека на те удобные, почти автоматические правила, которыми мы сейчас пользуемся. Нельзя было записывать и, следовательно, решать в общем виде алгебраические уравнения или какие-нибудь другие алгебраические выражения. Каждый вид уравнения с числовыми коэффициентами решался по особому правилу. Так, например, у Кардано рассматривались 66 видов алгебраических уравнений. Поэтому необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самих чисел не зависят.

Виет и его последователи установили, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной отрезка. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того же рода. Значит, их можно обозначать какими-либо отвлеченными знаками. Это и сделал Виет. Он не только ввёл свое буквенное исчисление, но сделал принципиально новое открытие, поставив перед собой цель изучать не числа, а действия над ними. Правда, у самого Виета алгебраические символы еще были мало похожи на наши. Например, кубическое уравнение Виет записывал так:

А cubus + В рlanum in A3 aequatur D solito.

Здесь ещё, как видим, много слов. Но ясно, что они уже играют роль наших символов. Такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Не случайно за это Виета называют "отцом" алгебры, основоположником буквенной символики.

К этому времени относятся свидетельства современников Виета о его огромной трудоспособности. Будучи чем-то увлечён, учёный мог работать по трое суток без сна.

Виет жил в эпоху кровопролитных религиозных войн. Франсуа Виет был католиком, но всё свое детство и отрочество провел в общине гугенотов — протестантского течения. Это воспитало в учёном большую веротерпимость и сделало его по большей части равнодушным к религии.

Это позволило ему без конфликтов уживаться и с протестантами, и с католиками, которые в то время враждовали, как в кругах аристократов, так и низших слоях общества.

Дружба с гугенотами могла стоить Виету и жизни — во время Варфоломеевской ночи он мог погибнуть, если бы тот момент оказался в усадьбе семьи де Партене.

По настоянию ярых католиков – герцогов Гизов – Виет был в конце 1584 года отстранён от должности и выслан из Парижа. После восшествия на престол Генриха IV, Виет в начале 1589г. стал советником парламента в городе Тур. Позднее он был назначен первым советником короля.

Именно на этот период приходится пик его творчества. Обретя неожиданный покой и отдых, учёный поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи. У него сложилось убеждение в том, «что должна существовать общая, неизвестная ещё наука, обнимающая и остроумные измышления новейших алгебраистов, и глубокие геометрические изыскания древних».

Виет изложил программу своих исследований и перечислил трактаты, объединённые общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом «Введении в аналитическое искусство». Перечисление шло в том порядке, в каком эти труды должны были издаваться, чтобы составить единое целое — новое направление в науке. К сожалению, единого целого не получилось. Трактаты публиковались в совершенно случайном порядке, и многие увидели свет только после смерти Виета. Один из трактатов вообще не найден. Однако главный замысел учёного замечательно удался: началось преобразование алгебры в мощное математическое исчисление. Само название «алгебра» Виет в своих трудах заменил словами «аналитическое искусство». Он писал в письме к де Партене: «Все математики знали, что под алгеброй и алмукабалой… скрыты несравненные сокровища, но не умели их найти. Задачи, которые они считали наиболее трудными, совершенно легко решаются десятками с помощью нашего искусства…»

Основу своего подхода Виет называл видовой логистикой. Следуя примеру древних, он чётко разграничивал числа, величины и отношения, собрав их в некую систему «видов». В эту систему входили, например, переменные, их корни, квадраты, кубы и т. д., а также множество скаляров, которым соответствовали реальные размеры — длина, площадь или объём. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных — согласные. Из знаков действий он использовал «+» и «—», знак радикала и горизонтальную черту для деления. Произведение обозначал словом «in». Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом. Но многие знаки, введённые до него, он не использовал. Так, квадрат, куб и т. д. обозначал словами или первыми буквами слов.

Виет обратил внимание на то, что Эвклид в своих трудах иногда обозначал длину отрезка буквой. Это натолкнуло учёного на смелую мысль: подразумевать под буквой также и число как количественную характеристику длины отрезка. Отсюда он сделал вывод, что можно выполнять разные действия не только над числами, но и над величинами, обозначенными буквами.

Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.

Может показаться, что Виет ввёл в символику алгеб¬ры совсем немного. Буквами для обозначения отрезков пользовались еще Евклид и Архимед, их успешно приме¬няли Леонардо Пизанский, Иордан Неморарий, Николай Орем, Лука Пачоли, Кардано, Бомбелли и многие другие математики. Но Виет сделал существенный шаг вперёд. Его символика позволила не только решать конкретные задачи, но и находить общие закономерности и полностью обосновывать их. Это, в свою очередь, способствовало выделению алгебры в самостоятельную ветвь математики, не зависящую от геометрии. Если предшественники Виета высказывали некоторые правила, рецептуры для решений конкретных задач и иллюстрировали их примерами, то Виет дал полное изложение вопросов, связанных с решением уравнений первых четырех степеней.

Виет, верный последователь древних, оперировал только рациональными положительными числами, которые он обозначал буквами. Если в результате подстановки в уравнение значений параметров неизвестное оказывалось иррациональным, он давал этому случаю особое обоснование.

Виет всюду делит изложение на две части: общие законы и их конкретно-числовые реализации. То есть, он сначала решает задачи в общем виде, и только потом приводит числовые примеры. В общей части он обозначает буквами не только неизвестные, но и все прочие параметры, для которых он придумал термин «коэффициенты» (буквально: содействующие). Виет использовал для этого только заглавные буквы — гласные для неизвестных, согласные для коэффициентов.

Виет свободно применяет разнообразные алгебраические преобразования — например, замену переменных или смену знака выражения при переносе его в другую часть уравнения. Это стоит отметить, принимая во внимание тогдашнее подозрительное отношение к отрицательным числам. Показатели степени у Виета ещё записываются словесно.

Франсуа Виета писал: «Искусство, которое я излагаю, ново или по крайней мере было настолько испорчено временем и искажено влиянием варваров, что я счел нужным придать ему совершенно новый вид».

Новая система позволила просто, ясно и компактно описать общие законы арифметики и алгоритмы. Символика Виета была сразу же оценена учёными разных стран, которые приступили к её совершенствованию. Среди непосредственных продолжателей дела создания символической алгебры можно назвать Хэрриота, Жирара и Отреда, практически современный вид алгебраический язык получил в XVII веке у Декарта.

В теории уравнений, решая уравнения высших степеней, Виет применил метод сведения данного уравнения к неполному уравнению при помощи некоторых подстановок. Он искал только положительные корни и использовал знак черты, поставленной над числовыми или буквенными выражениями, которая имела значение современных скобок.

Именем Виета названа самая знаменитая теорема школьного курса, в которой речь идет о взаимосвязи многочлена с его корнями. Теорема была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: «Если B+D, умноженное на А, минус А в квадрате равно BD, то А равно В и равно D» (гласная А в современных обозначениях отвечает неизвестной x, а согласные В и D – коэффициентам p и q квадратного уравнения x2 + px + q = 0).

Теорема Виета стала ныне самым знаменитым утверждением школьной алгебры. Если в школьной геометрии первое место прочно удерживает теорема Пифагора, то в школьной алгебре ведущая роль принадлежит формулам Виета: x1 + x2 = - p; x1 x2 = q.

Теорема достойна восхищения, особенно если учесть, что её можно обобщать на многочлены любых степеней.

Как и Пифагора, Виета в первую очередь помнят благодаря теореме, носящей его имя. Теорема Виета помогает не только школьникам и студентам, её так же часто используют университетские профессора, доктора наук, изобретатели. Она позволяет получать точные числа с меньшей затратой времени и сил, чем если бы уравнения решались стандартными способами и путями. Мало кто помнит теорему Виета после окончания школы, ещё меньше людей знают о том, что она касается решения не только квадратных уравнений. На самом деле это не теорема, а несколько формул, которые показывают связь коэффициентов многочлена и его корней.

Эти формулы были известны еще задолго до Виета. Так, ими пользовался итальянский математик Джероламо Кардано, который родился на 40 лет раньше знаменитого француза. Более того, подобные формулы были известны еще древним вавилонянам. Впрочем, это совсем не уменьшает заслуг Виета — он самостоятельно вывел свою теорему. В те времена часто происходили параллельные открытия.

Работы по математике Виет писал чрезвычайно трудным языком, поэтому они не получили распространения. Труды Виета были собраны после его смерти профессором математики в Лейдене Ф. Шоотеном.

Особенно гордился Виет всем известной теперь теоремой о выражении коэффициентов уравнения через его корни, полученной им самостоятельно, хотя, как теперь стало известно, зависимость между коэффициентами и корнями уравнения (даже более общего вида, чем квадратного) была известна Кардано, а в таком виде, в каком мы пользуемся для квадратного уравнения, - древним вавилонянам.

Знания тригонометрии Виет с успехом применял как в алгебре при решении алгебраических уравнений, так и в геометрии, например, при решении с помощью циркуля и линейки знаменитой задачи Аполлония Пергского о построении круга, касательного к трем данным кругам. Гордясь найденным решением, Виет называл себя Алоллонием Гальским (Галлией в старину называли Францию).

Больших успехов достиг учёный и в области геометрии. Применительно к ней он сумел разработать интересные методы. В трактате «Дополнения к геометрии» он стремился создать по примеру древних некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвёртой степеней. Любое уравнение третьей и четвёртой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.

Математиков в течение столетий интересовал вопрос решения треугольников, так как он диктовался нуждами астрономии, архитектуры, геодезии. У Виета применявшиеся ранее методы решения треугольников приобрели более законченный вид. Так он первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Было ясно сказано, что в этом случае решение не всегда возможно. Если же решение есть, то может быть одно или два.

Нельзя сказать, что во Франции о Виете ничего не знали. Громкую славу он получил при Генрихе III, во время франко-испанской войны.

При королевском дворе Виет проявил себя как талантливый специалист по расшифровке шифров, которыми пользовалась Испания в войне с Францией. Шифр состоял из 500 символов (по другим сведениям – содержал до 600 различных знаков). Генрих IV обратился к Виету с просьбой разгадать шифр. В течение двух недель, дни и ночи работал Виет и разгадал тайну испанского шифра. После этого неожиданно для испанцев Франция стала выигрывать одно сражение за другим. Испанцы долго недоумевали. Наконец им стало известно, что шифр для французов уже не секрет и что виновник его расшифровки - Виет. Будучи уверенными в невозможности разгадать их способ тайнописи людьми, они обвинили Францию перед папой римским и инквизицией в кознях дьявола, а Виет был обвинен в союзе с дьяволом и заочно приговорен к сожжению на костре.

Католическая церковь не терпела инакомыслия. На протяжении столетий в феодальном мире костры инквизиции пылали там, где пробивались ростки нового, передового, торжествовал разум. Широко использовались доносы и лжесвидетельства. Донос вменялся в обязанность верующим и щедро вознаграждался из имущества осужденных. Имена свидетелей, а ими могли стать взрослые и малые дети, друзья и враги, верующие и еретики, убийцы и клятвопреступники, также оставались втайне. От суда инквизиции не спасали социальное положение, пол, возраст и даже смерть. От обвиняемого требовали раскаяния, которое не исключало наказание.

Тюремное заключение чаще всего было пожизненным. Заключенные содержались в полной изоляции, их заковывали в кандалы, кормили только хлебом и водой. Наиболее жестоко свирепствовала инквизиция в Испании в течение трех с половиной столетий. Аутодафе (дело веры) достигло в Испании грандиозных размеров, стали своеобразными театрализованными представлениями. Их приурочивали к большим церковным праздникам, торжественным государственным актам. За 50 лет с 1550 по1600 год только в Италии было сожжено 78 ученых вместе с их трудами. Научную мысль душили изощренно и беспощадно. Но развитие науки и свободную мысль остановить нельзя. Это доказывает жизнь и судьба ученых того времени: Николая Коперника, Джордано Бруно и Галилео Галилея.

Исполнить приговор испанцы не смогли. Генрих IV спрятал Виета в одном из провинциальных городков Франции.

Ф.Виет дал основы общей теории алгебраических уравнений, стал крупнейшим французским математиком 16-го века. Благодаря работам Виета стало возможным выражение корней уравнений общими формулами.

Виет нашёл общие методы решений уравнений второй, третьей и четвертой степеней, усовершенствовал методы Ферро и Феррари, вывел известные теперь каждому школьнику формулы Виета.

Свои исследования по математике Виет опубликовал в книге „Математический канон” (1579), а результаты изучения трудов Архимеда, Евклида, Аполлония, Диофанта, Кардано в 1584-1589 г.г. в основном своем труде „Искусство анализа”.

Виет улучшил результат Архимеда: используя представление о круге как о пределе вписанных в него многоугольников при увеличении числа их сторон, он вычислил число π до 18-го знака после запятой (из них 11 знаков оказались верными).

Значительным достижением учёного было представление числа π в виде бесконечного произведения. Это был первый случай использования бесконечных произведений, которыми спустя почти два столетия блестяще пользовался Леонард Эйлер.

Франсуа Виету удалось выразить число бесконечным произведением радикалов:

При выводе своей формулы Виет исходил из следующего свойства правильных вписанных в круг единичного радиуса многоугольников:

, где Sk, S2k --площади правильных вписанных в круг единичного радиуса k -угольника и 2k -угольника; hk --апофема k-угольника. Отсюда

Между апофемами h2k и hk правильных вписанных в круг единичного радиуса 2k- и k-угольника существует следующая связь:

Её можно получить из соотношения

между апофемой h и стороной a правильного вписанного в круг единичного радиуса многоугольника. Поскольку , то из предыдущего равенства получаем:

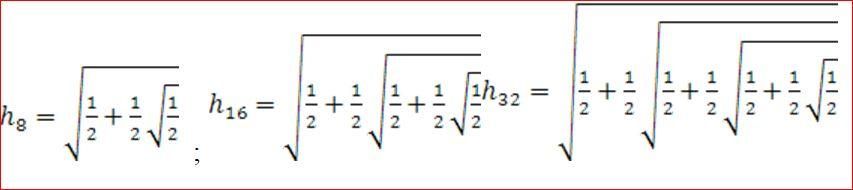
И т. д.

Как талантливый вычислитель, Виет разработал метод приближённого решения алгебраических уравнений с числовыми коэффициентами, который применялся до конца 17 ст., пока Ньютон не нашёл более совершенный метод.

В тригонометрии он нашёл полное решение плоского и сферического треугольника по трём данным элементам.

В 1589 году, после убийства Генриха Гиза по приказу короля, Виет возвратился в Париж. Но в том же году Генрих III был убит монахом — приверженцем Гизов. Формально французская корона перешла к Генриху Наваррскому — главе гугенотов. Но лишь после того, как в 1593 году этот правитель принял католичество, в Париже его признали королём Генрихом IV. Так был положен конец кровавой и истребительной религиозной войне, долгое время оказывавшей влияние на жизнь каждого француза, даже вовсе не интересовавшегося ни политикой, ни религией.

Подробности жизни Виета в тот период неизвестны, что само по себе говорит о его желании оставаться в стороне от кровавых дворцовых событий. Известно только, что он перешёл на службу к Генриху IV, находился при дворе, был ответственным правительственным чиновником и пользовался огромным уважением как математик.

Виет за свой счёт опубликовал множество трудов, свидетельствующих о всесторонности его знаний. Он рассылал эти труды почти во все университеты европейских стран. Но математический язык этих сочинений был столь трудным, что работы не получили той оценки, которую заслуживали.

Работы Ф. Виета произвели настоящую революцию в алгебре, но только после его смерти лейденский профессор Франц Шостен издал его труды под заголовком «Орега Vietal». Виету удалось перешагнуть из шестнадцатого в двадцатый век: он говорил, что надо изучать не сами числа, а действия над ними. Это изменило всю философию математики.

По преданию, посол Нидерландов сказал на приёме у короля Франции Генриха IV, что их математик Адриен ван Ромен задал математикам задачу: решить уравнение 45-ой степени:

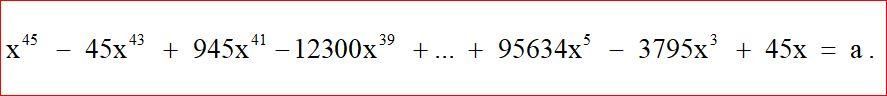
Он разослал во все европейские страны это уравнение, а французским математикам решил это уравнение не посылать, считая, что там нет способных справиться с задачей: Декарт в то время ещё не родился, Пьера Рамуса в 1572 убили в Варфоломеевскую ночь, а о других математиках не было слышно. Генрих IV ответил, что во Франции есть математик, и пригласил Виета. Виет тут же, в присутствие короля, министров и гостей, нашёл один корень предложенного уравнения. Виет увидел, что а есть сторона правильного 15-угольника, вписанного в круг радиуса 1, а по коэффициентам второго и последнего членов заключил, что х есть хорда 1/45 этой дуги, как оно и было на самом деле. На следующий день он нашёл ещё 22 положительных корня предложенного уравнения (отрицательных и мнимых корней он не признавал). Убелённый сединами 53 - летний красавец Виет заслужил не только аплодисменты двора, но и восхищение Ромена. Между ними установилась крепкая дружба.

Как и многие выдающиеся учёные, Виет отличался большой работоспособностью. В течение большей части своей жизни он был так загружен юридической деятельностью, что трудно представить, где он находил время для основательного изучения древних авторов и написания больших математических работ. Труды Виета были собраны и опубликованы в 1646 году.

Виет первым употребил фигурные скобки, первым рассмотрел бесконечное произведение, предложил для приближенного решения уравнений с числовым коэффициентами новый метод, сходный с тем, который позднее предложил И.Ньютон. Усовершенствование техники было результатом усовершенствования обозначений. Известно, что новые результаты часто становятся возможными лишь благодаря новому способу записи. За усовершенствованием обозначений Виета поколение спустя последовало применение алгебры к геометрии у Декарта.

Среди научных заслуг Виета: полное аналитическое изложение теории уравнений первых четырёх степеней; идея применения трансцендентных функций к решению алгебраических уравнений; оригинальный метод приближённого решения алгебраических уравнений; частичное решение задачи Аполлония о построении круга, касающегося трёх данных, в сочинении Apollonius Gallus (1600). Решение Виета не подходит для случая внешних касаний.

В последние годы жизни Виет ушёл с государственной службы, но продолжал интересоваться наукой. Известно, например, что он вступил в полемику по поводу введения нового, григорианского календаря в Европе. И даже хотел создать свой календарь.

Ф.Виет оставался при дворе короля Франции до самой смерти. Незадолго до смерти Виет заболел и отошёл от работы. Существует версия, согласно которой агенты инквизиции всё-таки отомстили за расшифрованные коды и тайно убили учёного...

В придворных новостях маркиз Летуаль писал «…13 декабря 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых учёных математиков века умер в Париже, имея, по общему мнению, 20 тысяч экю в изголовье. Ему было более 60 лет».

Фото ученого, конечно же, не существует. Но художники-современники часто писали портреты Виета. Благодаря им мы имеем возможность увидеть человека, подарившего нам алгебру. Судя по портретам, Франсуа носил бороду и одевался весьма стильно для того времени.

В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: «…14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых учёных математиков века умер… в Париже, имея, по общему мнению, 20 тыс. экю в изголовье. Ему было более шестидесяти лет».

Датский историк математики Г. Г. Цейтен (1839—1920) писал: «Виет в течение большей части своей жизни так был занят своей юридической деятельностью, что трудно представить себе, как он справлялся со своими большими математическими работами, являющимися плодом глубоких математических исследований и свидетельствующими об основательном изучении древних авторов. Рассказывают, что он мог проводить за своим рабочим столом над занимавшими его исследованиями по трое суток сряду».

Использование трудов Виета очень затруднялось тяжёлым и громоздким изложением. Как отмечал тот же Г. Г. Цейтон, чтение его работ затрудняется несколько изысканной формой, в которой повсюду сквозит его большая эрудиция, и большим количеством изобретённых им и совершенно не привившихся греческих терминов. Из-за этого они полностью не изданы до сих пор. Сборник трудов Виета был издан посмертно (1646, Лейден) его голландским другом Ф. ван Схотеном.

В честь Франсуа Виета в 1935 г. назван кратер на видимой стороне Луны.

Символики Виета придерживался впоследствии Пьер Ферма. Дальнейшее значительное усовершенствование алгебраической символики принадлежит Декарту. Рене Декарт ввёл для обозначения коэффициентов строчные буквы латинского алфавита. Для обозначения неизвестных он использовал последние буквы того же алфавита. Это нововведение получило широкое распространение в работах математиков и с небольшими изменениями сохранилось до наших дней.

Интересные факты из жизни и деятельности Виета:

• Франсуа Виет, вычисляя периметры вписанного и описанного 322 216-угольников, получил 9 точных десятичных знаков.

• Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4).

• Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы.

• Ученый мог работать по трое суток без сна!

• Теорему Виета можно обобщить на многочлены любой степени.

• Непосредственно применение трудов Виета очень затруднялось тяжелым и громоздким изложением. Из-за этого они полностью не изданы до сих пор.

• Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом.

• Придумал новый тригонометрический метод решения неприводимого кубического уравнения, применимый также для трисекции угла.

• Придумал первый пример бесконечного произведения.

• Вывел формулы для синусов и косинусов кратных углов, т.е. формул для sin(mx) и cos(mx), дающие разложения по степеням sinx и cosx.

• Вычислил число π до 11-го верного знака после запятой.

• Виет разработал метод приближённого решения алгебраических уравнений с числовыми коэффициентами, который применялся до конца 17 столетия, пока И. Ньютон не нашёл более совершенный метод.

• Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры - стало возможным буквенное исчисление.

• Произведение Виет обозначал словом «in».

• Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.

• Он первым явно сформулировал в словесной форме теорему косинусов.

О теореме Виета сложены стихи. Вот одно из них:

И. Дырченко

Задача Виета

Решить уравнение х2 + px + q = 0 подстановкой x = y + z.

Дополнение

Формулы, выведенные Виетом для квадратных уравнений, верны и для многочленов высших степеней.

Пусть многочлен

P(x) = a0xn + a1xn-1¬¬¬ + … +an имеет n различных корней x1 , x2 …, xn.

В этом случае он имеет разложение на множители вида:

a0xn + a1xn-1 +…+ an = a0( x – x1)( x – x2)…(x – xn)

Разделим обе части этого равенства на a0 ≠ 0 и раскроем в первой части скобки. Получим равенство:

xn + ( )xn-1 + … + ( ) = xn – (x1 + x2 + … + xn) xn-1 + ( x1x2 + x2x3 + … +

xn-1xn)xn-2 + … +(-1)n x1x2 … xn

Но два многочлена тождественно равны в том и только в том случае, когда коэффициенты при одинаковых степенях равны. Отсюда следует, что выполняется равенство

x1 + x2 + … + xn = -

x1x2 + x2x3 + … + xn-1xn =

x1x2 … xn = (-1)n

Например, для многочленов третей степени

a0x³ + a1x² + a2x + a3 имеем тождества

x1 + x2 + x3 = -

x1x2 + x1x3 + x2x3 =

x1x2x3 = -

Как и для квадратных уравнений, эти формулы называют формулами Виета.

Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.