"Отец" математической логики

Один из основателей математической логики Джордж Буль (George Boole) родился 2 ноября 1815 года в Линкольне, Линкольншир, Англия в семье небогатого ремесленника Джона Буля.

Предками Джорджа были фермеры, а так же мелкие ремесленники. Начиная с XVI в., фамилия Boole (являющаяся старым вариантом написания 'Bull' - бык) впервые появляется в записях в районах юго-западнее Скегнесса.

Отец Джорджа, Джон Буль, держал сапожную мастерскую, а мать Мэри до той поры, пока не вышла замуж, была камеристкой. Однако, сапожному делу, служившему источником пропитания для семьи, в которой было четверо детей, отец уделял значительно меньше внимания, чем своему главному увлечению – изготовлению различных оптических приборов.

Отец будущего учёного был добрым, глубоко религиозным человеком. Мать Джорджа на вопрос, чем занимался отец её знаменитого сына, кратко ответила: «Он был философ».

Буль-младший обожал отца и с детских лет помогал ему шлифовать линзы и делать другую нехитрую механическую работу. Образование мальчик получил соответственно достатку семьи: окончил местную начальную школу, научившись писать и считать. Однажды мальчик не явился на занятия. Его разыскали в городе, где он зарабатывал свои первые деньги. Джордж безошибочно говорил по буквам труднопроизносимые слова, а люди в восторге бросали ему деньги.

К восьми годам мальчика всецело захватила жажда знаний. Предметом, который, по-видимому, сыграл важную роль в дальнейшей судьбе Буля, был латинский язык. Здесь отец ничем не мог ему помочь, но друг их семьи, занимавшийся книжной торговлей, в достаточной степени владел латинской грамматикой, чтобы дать Булю начальный толчок. Когда книготорговец обучил его всему, что знал сам, Буль продолжил учёбу самостоятельно и в возрасте 12 лет уже переводил классическую латинскую поэзию. Ещё через два года он овладел греческим языком, а затем добавил к своей коллекции языков французский, немецкий и итальянский.

У него была почти фотографическая память. "Мой мозг устроен таким образом, – писал он впоследствии, – что любые факты или идеи, о которых я узнавал, запечатлевались в нём подобно хорошо упорядоченной группе рисунков".

В возрасте 16 лет Буль был вынужден поступить на работу, чтобы помочь семье. Четыре года он проработал на малооплачиваемой должности помощника учителя в частной школе в Донкастере, в предместье Лондона. Через два года, в 1833 г. он, однако, покинул Донкастер. Это случилось, когда директору школы стало известно, что младший учитель принадлежит к унитарной церкви, занимается математикой по воскресеньям и даже в церкви решает математические задачи.

Впрочем, была еще одна причина ухода из школы. Как вспоминал один из его коллег, "она состояла в том, что Буль был полностью поглощён своими собственными мыслями, и в такой степени "отсутствовал", что мальчики начинали плутовать. Он был превосходным учителем, если видел, что ребенок понимает его (у него было два таких ученика)… Но для большинства детей, не проявлявших рвения в учёбе и нуждавшихся в непрерывном натаскивании, он был самым плохим учителем из тех, кого я когда-либо встречал. Вместо объяснений он выходил из себя и с раздражением отправлял ученика прочь – а парнишка только и ждал этого, чтобы уйти с урока. Ученики подсовывали ему работы, которые были выполнены другими, или несколько раз показывали ему одно и то же задание, а если они говорили, что у них всё выполнено правильно, он охотно верил этому и снова углублялся в свои книги… Во всем остальном его ценили очень высоко, настолько высоко, насколько это возможно".

Новую работу Джордж нашёл в Ливерпуле, в учебном заведении некоего Марро. Однако через 6 месяцев, не выдержав, по собственному признанию, "творившегося там хаоса", перебрался в родной город и основал маленькую школу-пансион. В это время Джорджу было только 19 лет!

После открытия собственной школы, Буль понял, что ему следует углубить свои познания в математике, чтобы превзойти учеников, и приступил к чтению математических журналов, которые имелись в библиотеке местного научного учреждения. Он внимательнейшим образом штудирует Ньютоновы «Philosophiae Naturalis Principia» и «Механику» Лагранжа, сличая, попутно, методы обоих ученых. Представьте себе трудности молодого человека, знакомого лишь с началами математики и пытающегося понять утверждения, которые часто приводились без доказательств, предваряясь сакраментальным: "легко видеть, что…" (тем более что книги великих французов он изучал в оригинале).

Изучив горы научных публикаций, он овладел сложнейшими математическими теориями своего времени. У него возникли и собственные оригинальные идеи. Буль стал записывать их, не прекращая в то же время преподавательской работы в своей маленькой школе.

Одна из первых его работ (по анализу) в силу неизвестности автора и сложности вопроса чуть не была отклонена от публикации, но через два года за эту работу Булю присудили Королевскую медаль Королевского научного общества, причём это был первый случай, когда медаль вручалась за чисто математическую работу.

Но школа давала слишком скромный доход, а ведь юноша был по сути кормильцем семьи. И в 1838 году Джорджу Булю с готовностью принял предложение возглавить после смерти основателя и директора Роберта Холла Академию для детей состоятельных фермеров в Ваддингтоне, небольшом городке под Линкольном, куда вместе с родителями, двумя братьями и сестрой Джордж и перебрался. Семейство стало совместно заведовать делами школы, что помогло решить финансовые проблемы.

Но молодой учёный к этому времени уже имел свои собственные идеи о том, каким должно быть образование. Ещё во время существования его первой линкольнской школы он написал эссе, в котором рассуждал об этом. Буль настаивал на необходимости прежде всего понимать, а не запоминать материал – идея на тот момент не такая уж и распространенная.

Кроме того, он утверждал, что в воспитании нужно большое внимание уделять формированию морально-этических ценностей, и полагал этот аспект работы педагога наиболее трудным, но и при этом наиболее важным. Поэтому, по мере улучшения материального положения семьи, Джордж все чаще и чаще возвращался к идее создания собственной академии.

Облик Буля как педагога рисует Р. Рис. Он приводит воспоминания ученика Буля Р. А. Джемисона, который пишет, что Буль часто стремился к тому, чтобы его слушатели смогли сами заново открывать некоторые из уже полученных другими учёными результатов (а не излагал их все на своих лекциях). "Он приучал нас, – продолжает вспоминать Джемисон, – почувствовать “радость открытия”".

А вот воспоминания других студентов Буля. "Секрет его успеха, я думаю, состоял в том, что он, кажется, никогда не повторял или воспроизводил то, что однажды изучил сам, и всегда стремился к тому, чтобы создавалось впечатление, что он получает результат во время лекции, и что студенты участвуют в этом вместе с ним, и вместе с ним разделяют честь открытия".

"Мы никогда не чувствовали, что находимся в присутствии человека, являющегося знатоком математики – скорее в присутствии человека, который, как и мы, является учеником, постигающим математические истины. Он опускался до уровня наших знаний, и мы двигались дальше одновременно с ним. Хотя мы знали, что он излагает известные ему идеи, казалось, что он не использует заранее подготовленный и выверенный набор фраз или задач. Лекция фактически читалась так, что создавалось впечатление, что именно в этот момент его посещают некоторые оригинальные идеи. Иногда, развивая их, он, казалось, вообще забывал о нашем присутствии...".

"Он с большой тщательностью готовил большой список вопросов и задач, начиная с азов и кончая высшими разделами математики, которые время от времени печатал и раздавал студентам. Он любил повторять, что пока эти примеры не решены, нельзя говорить о большом прогрессе в изучении предмета, и то, что было усвоено на лекциях, вскоре будет забыто".

"Любителям алгебраического анализа доставляло истинное удовольствие наблюдать за тем, как некоторые основополагающие математические принципы становились понятными после того, как он исписывал одну доску за другой своими формулами. Каждый раз, когда он при этом доходил до пункта, важного для получения конечного результата, его лицо озарялось радостной улыбкой удовлетворения, и когда он с надеждой задавал аудитории вопрос: "Можете ли вы дальше продолжить самостоятельно?" – то обычно получал положительный ответ. Но если слышал: "Мы не поняли этот или тот пункт", – никогда не раздражался, а спокойно объяснял снова и снова, используя другие средства или рисунки, или прибегая к помощи тех, которые уже поняли проблему...".

О том, как студенты уважали и любили своего профессора, свидетельствует такой эпизод. Однажды он пришел в аудиторию задолго до начала лекции, и, повернувшись лицом к доске, углубился в размышления. Аудитория постепенно заполнялась студентами, которые вели себя очень тихо, чтобы не помешать профессору. Время шло, а Буль продолжал стоять спиной к студентам. Лекционный час истек, и студенты также тихо, как входили и рассаживались, покинули аудиторию. Когда Буль пришел домой, он сказал жене: "Моя дорогая, сегодня произошло экстраординарное событие – никто из моих студентов не пришел на лекцию".

На протяжении следующего десятилетия работы Буля регулярно печатались, и его имя приобрело известность в научных кругах. В конце концов, деятельность Буля получила столь высокую оценку, что он, несмотря на отсутствие формального образования, был приглашен работать в Ирландии. В 1849 году в городе Корк (Ирландия) открылось новое высшее учебное заведение – Куинз колледж. По рекомендации коллег-математиков Буль получил здесь профессуру, которую сохранил до своей смерти.

В сорок лет он женился на Мери Эверест, которая была на 17 лет моложе его и была племянницей знаменитого географа Джорджа Эвереста. После смерти мужа она много сил потратила на популяризацию его вклада в логику.

У них было пять дочерей. Четыре их дочери снискали известность как учёные (геометр Алисия, первая женщина - профессор химии в Лондоне Люси), или члены учёных семей (Мэри, жена математика и писателя Ч. Г. Хинтона, и Маргарет, мать математика Дж. И. Тейлора), а пятая, младшая — Этель Лилиан Войнич — прославилась как писатель, автор известного романа "Овод" (скончалась в Нью-Йорке в возрасте 95 лет).

Современники отмечают демократические привычки Буля, отсутствие у него какого бы то ни было почтения к установившимся в Британии социальным предрассудкам и барьерам, указывают на его принципиальный характер и развитое чувство юмора.

Буль отличался большой независимостью и оригинальностью ума, но при жизни был малоизвестен. Он был известен в основном как автор ряда трудных для понимания статей на математические темы и трёх или четырёх монографий, ставших классическими.

Публикация первой статьи («Теория математических преобразований», 1839) привела к дружбе между Булем и Д. Ф. Грегори, редактором «Кембриджского математического журнала», где статья была опубликована, продолжавшейся до самой смерти последнего в 1844 г. (Дункано Ф. Грегори, молодой кембриджский алгебраист, принадлежал к знаменитой шотландской семье, которая дала миру Джеймса Грегори (1638-1675), изобретшего рефракционный телескоп и доказавшего сходимость ряда для числа π, и Дэвида Грегори (1659-1708) – математика, оптика, астронома, друга Ньютона). В этот журнал и наследовавший ему «Кембриджский и дублинский математический журнал» Буль представил двадцать две статьи.

Ободренный поддержкой Грегори, Джордж в течение нескольких лет публикует в том же журнале статьи по операторным методам анализа, теории дифференциальных уравнений и алгебраических инвариантов (1841). Пожалуй, это самое замечательное достижение молодого Буля: не будь теории инвариантов, развитой впоследствии Артуром Кэли и Джеймсом Сильвестром, возможно, "не состоялась" бы и теория относительности Альберта Эйнштейна.

В 1842 году Джордж отправил именитому математику Августу де Моргану (наставнику Ады Лавлейс (Байрон)) работу «Об общем методе анализа, применяющего алгебраические методы для решения дифференциальных уравнений». Морган добился публикации этой статьи в материалах Королевского общества, и она была удостоена медали Общества за вклад в развитие математического анализа.

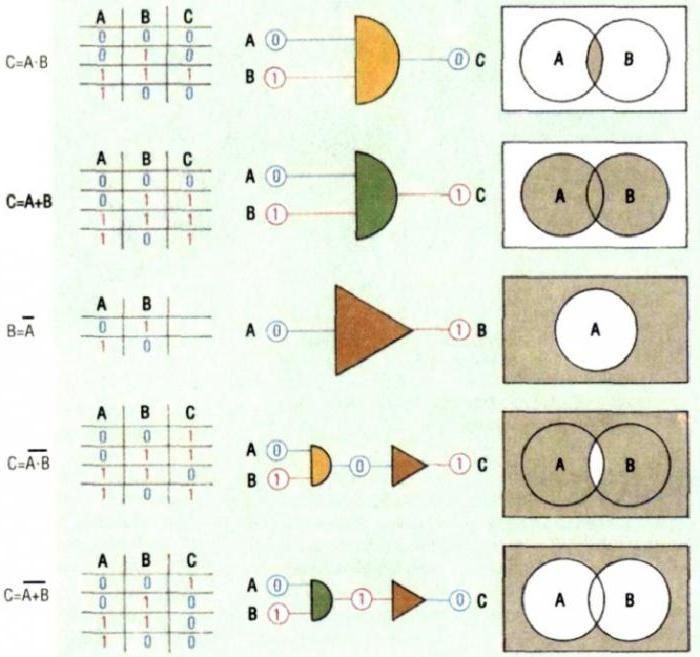
Основные труды Буля посвящены высшей алгебре, теории вероятностей, теории дифференциальных уравнений, исчислению конечных разностей. Но наибольшее значение имеет созданная Булем символическая математическая логика. Изобретённая им алгебра - булева алгебра - стала универсальным языком для описания всех логических процессов, в том числе и электронных вычислительных машин. Теория логики Буля, основанная на трех основных действиях — AND (и), OR (или), NOT (не), — должна была стать в XX веке основой для разработки переключающих телефонных линий и проекта ЭВМ. Так же, как и идеями Лейбница, булевой алгеброй пренебрегали в течение многих лет после того, как она была создана.

Важность работы, признанной логиком де Морганом, современником Буля, заключалась в следующем: “Символические процессы алгебры, созданные как инструменты числового вычисления, компетентно выражают каждый закон мысли и обладают грамматикой и словарем всего того, что содержит систему логики. Мы это и не предполагали, пока это не было доказано в “Законах мышления”".

Если Лейбниц в своё время пытался арифметизировать логику, то Буль её алгебраизирует, превращая в математическую науку. В принципе, его идеи лежали в русле попыток английских алгебраистов создать символическую алгебру, т. е. "науку о символах и их комбинациях, конструируемых по их собственным правилам, которая может быть применена к арифметике или к другим наукам посредством интерпретации" (Д. Пикок).

Джордж Буль по праву считается «отцом» математической логики. Его монографии «Математический анализ логики», «Исследование законов мышления» стали классическими. В научных трудах Буля отразилось его убеждение о возможности изучения свойств математических операций, осуществляемых не обязательно над числами. Буль был, вероятно, первым после Джона Валлиса математиком, обратившимся к логической проблематике.

Идеи применения символического метода к логике впервые высказаны им в статье «Математический анализ логики» (1847).

Занятия Буля логикой были в значительной степени стимулированы дискуссией между А. Де Морганом и У. Гамильтоном, за которой он с интересом следил весной 1847 г. Буль сам отмечает это обстоятельство в предисловии к “Математическому анализу логики”, написанному в октябре 1847 г. Он признает также, что А. Де Морган был первым логиком, обратившимся к анализу количественно определяемых предложений.

Де Морган восторженно приветствовал попытку Буля применить алгебраические методы для решения задач логики. "Я полагаю, – писал он, – что именно м-р Буль установил истинную связь алгебры и логики". И далее: "Система логики Буля – одно из многих свидетельств объединенных усилий гениальности и терпения…. Операции над алгебраическими символами, изобретенные в качестве средства числовых вычислений, достаточны для выражения любых движений мысли и предоставляют собой грамматику и словарь законченной логической системы…

Когда Гоббс во времена Республики (Commonwealth) опубликовал книгу "Вычисления или Логика", он имел смутное представление о некоторых вопросах, которые получили освещение в дни м-ра Буля. Однако единство форм мышления во всех разнообразных проявлениях разума не было достигнуто и стало предметом, вызвавшим всеобщий интерес. Имя м-ра Буля всегда будут помнить в связи с тем, что им сделаны наиболее значительные шаги в этом направлении".

Не удовлетворённый полученными в ней результатами, Буль высказывал пожелание, чтобы о его взглядах судили по обширному трактату «Исследование законов мышления, на которых основываются математические теории логики и вероятностей» (1854).

Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. Единицей Буль обозначал универсум мыслимых объектов, буквенными символами — выборки из него, связанные с обычными прилагательными и существительными (так, если x="рогатые", а y="овцы", последовательный выбор x и y из единицы даст класс рогатых овец).

Буль показал, что символика такого рода подчиняется тем же законам, что и алгебраическая, из чего следовало, что их можно складывать, вычитать, умножать и даже делить. В такой символике высказывания могут быть сведены к форме уравнений, а заключение из двух посылок силлогизма — получено путём исключения среднего термина по обычным алгебраическим правилам.

Ещё более оригинальной и примечательной была часть его системы, представленной в «Законах мышления…», образующая общий символический метод логического вывода. Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций. Вторая часть «Законов мышления…» содержит аналогичную попытку обнаружить общий метод в исчислении вероятностей, позволяющий из заданных вероятностей совокупности событий определить вероятность любого другого события, логически связанного с ними.

На достижения Буля частично опирались математические открытия, к тому времени появившиеся в Англии, в том числе и идеи Чарльза Бэббиджа, изобретателя первой аналитической вычислительной машины. Математики обратили внимание на идею Бэббиджа о математических операциях и величинах, использующихся в них. Идея стала возможной благодаря группе британских специалистов в области алгебры, к которым принадлежал и Буль.

Буль продемонстрировал, что логика может сводиться к очень простым ал¬гебраическим системам, после чего для Бэббиджа и его последователей ста-ло возможным создание механических устройств, которые могли решать необходимые логические задачи.

Базовым понятием булевой алгебры является понятие высказывания, под которым понимается любое утверждение, рассматриваемое только с точки зрения его истинности или ложности. В булевой алгебре не существует истинно-ложных или ложно-истинных высказываний. Высказывание можно рассматривать как логическую переменную, которая может принимать различные значения, например, высказывание “сегодня понедельник” будет истинным в понедельник и ложным во все остальные дни недели. Исчисление высказываний как раз и основано на том, что их можно рассматривать как двоичные переменные, которые могут принимать одно из двух своих значений. Примерами двоичных логических переменных являются разряды чисел, представленных в двоичной системе счисления; замкнутый или разомкнутый контакт; наличие или отсутствие тока в цепи; высокий или низкий потенциал в какой-либо точке схемы и т.п.

Большинство логиков того времени либо игнорировали, либо резко критиковали систему Буля, но её возможности оказались настолько велики, что она не могла долго оставаться без внимания. Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Это первым из ученых осознал американский логик Чарлз Сандерс Пирс и применил теорию для описания электрических переключательных схем.

Сегодня идеи Буля используются во всех современных цифровых устройствах.

Буль занимался и традиционными математическими дисциплинами. Так, в 1859 году он написал работу, посвященную дифференциальным уравнениям, а в 1860 году — вычислениям конечных разностей. Также он занимался теорией вероятностей, а всего им было написано свыше 50 работ.

Занимаясь математическими исследованиями, учёный не забывал о гуманитарных предметах. Буля интересовали лингвистика и логика, философия, этика и поэзия. Буль продолжал сочинять поэтические произведения, классические по форме и философские по содержанию. Ему принадлежат два стихотворения (“Сонет к числу три” и “Звание мертвеца”).

Этот слишком большой разброс интересов профессора математики его супруга, видимо, не одобряла. Она самым решительным образом покончила с его поэтическими упражнениями: однажды забрала у него листы, на которых он писал стихи, и кинула их в огонь.

Его имя увековечено в названиях многих математических понятий (булевы кольца, булевы алгебры, булево пространство и т.д.)

Смерть Джорджа Буля была очень неожиданной. Он был полон сил, энергии, много работал, еще больше планировал сделать. Опасение внушали только некоторые проблемы с легкими, которые появились после переезда в Корк – город с более влажным климатом, чем Линкольн. 24 ноября 1864 года случилось, казалось бы, вполне заурядное событие, которое в итоге привело к трагическим последствиям. В проливной дождь Буль прошёл две мили, отделявшие его дом от колледжа, и хотя промок до нитки, добросовестный профессор не стал отменять лекций, а провёл их в мокрой одежде, из-за чего сильно простудился. Вскоре простуда перешла в воспаление лёгких. Говорят, что для ухода за мужем Мария использовала модную в те времена гомеопатию, утверждающую, что болезнь можно вылечить с помощью средства, вызвавшего эту болезнь, т.е. "клин клином вышибают". В результате, Джорджа Буля оборачивают в мокрой простыни. Поэтому не странно, что победить болезнь не удалось, и 8 декабря1864 года Джордж Буль умер. Он был похоронен в церкви Ирландии кладбища Святого Михаила (пригород Корка).

Лучшей эпитафией для Буля были бы слова знаменитого логика и философа Бертрана Рассела: "Чистая математика была открыта Булем в работе, которую он назвал "Законы мышления".

Логические идеи Буля в последующие годы получили дальнейшее развитие. Логические исчисления, построенные в соответствии с идеями Буля, находят сейчас широкое применение в приложениях математической логики к технике, в частности к теории релейно-контактных схем. В современной алгебре есть булевы кольца, булевы алгебры - алгебраические системы, законы композиции которых берут своё начало от исчисления Буля. В общей топологии известно булево пространство, в математических проблемах управляющих систем - булев разброс, булево разложение, булева регулярная точка ядра.

Рассказывают, что…

• Как уже упоминалось, жена Буля была племянницей Джорджа Эвереста, в 1841 году завершившего в Индии грандиозные по масштабам работы.

В честь его заслуг высочайшая вершина мира Джомолунгма в Гималаях одно время даже именовалась Эверестом. Сама Мэри, в отличие от жен многих других математиков, понимала научные идеи своего мужа и своим вниманием и участием подвигала его на продолжение исследований. После его смер¬ти она написала несколько сочинений и в последнем из них — “Философия и развлечения алгебры”, — опубликованном в 1909 году, пропагандировала математические идеи Джорджа.

У четы Булей было пять дочерей. Старшая, Мэри, вышла замуж за Ч. Хинтона — математика, изобретателя и писателя-фантаста — автора широко известной повести “Случай в Флатландии”, где описаны некие существа, живущие в плоском двумерном мире. Из многочисленного потомства Хинтонов трое внуков стали учёными: Говард — энтомологом, а Вильям и Джоан — физиками. Джоан была одной из немногих женщин-физиков, принимавших участие в работе над атомным проектом в США.

Вторая дочь Булей, Маргарет, вошла в историю как мать крупнейшего английского механика и математика, иностранного члена Академии наук СССР Джеффри Тэйлора. Третья, Алисия, специализировалась в исследовании многомерных пространств и получила почётную ученую степень в Гронингенском университете. Четвертая, Люси, стала первой в Англии женщиной-профессором, возглавившей кафедру химии.

Но наиболее известной из всех дочерей Булей стала младшая, Этель Лилиан, вышедшая замуж за ученого — эмигранта из Польши Войнича. Войдя в революционную эмигрантскую среду, она написала прославивший её на весь мир роман “Овод”. За ним последовало ещё несколько романов и музыкальных произведений, а также перевод на английский язык стихотворений Тараса Шевченко. Войнич скончалась в Нью-Йорке в возрасте 95 лет, немного не дожив до столетия со дня смерти своего знаменитого отца математика Джорджа Буля.

• Американский логик Чарльз Сандерс Пирс через двенадцать лет после публикации Булем «Исследований законов мышления» произнёс краткую речь, описывавшую идею Буля Американской академии искусств и наук, а затем провёл более 20 лет, изменяя и расширяя её, чтобы реализовать потенциал теории на практике. Это привело к проектированию базовой электрической логической схемы. Пирс свою теоретическую логическую схему в действительности так никогда и не построил, так как был больше учёным, чем электриком, но ввёл Булеву алгебру в университетские курсы логической философии. В конце концов, один одарённый студент, Клод Шеннон, взял эту идею и развил её.

Приложения:

1. Булева алгебра

Булевой алгеброй называется произвольное множество элементов a, b, c, ... , для которых определены две операции - сложение и умножение, сопоставляющие каждым двум элементам a и b их сумму a + b и произведение a b ; определена операция "отрицание", сопоставляющая каждому элементу a новый элемент (-a) ; имеются два "особых" элементов 0 и 1 и выполняются следующие правила:

• коммутативные законы: a + b = b + a ; a b = b a

• ассоциативные законы: ( a + b ) + c = a + ( b + c ) ; ( a b ) c = a ( b c )

• идемпотентные законы: a + a = a ; a a = a

• дистрибутивные законы: ( a + b ) c = a c + b c ; a b + c = ( a + c )( b + c )

• отрицание отрицания: (-(-a)) = a

• для 0 : a + 0 = a ; a 0 = 0 ; (-0) = 1

• для 1 : a + 1 = 1 ; a 1 = a ; (-1) = 0

• правила де Моргана: (-( a + b )) = (-a) (-b) ; (-( a b )) = (-a) + (-b).

Замечание 1. Для определения алгебры Буля можно обойтись лишь одной из операцией сложения или умножения вместе с операцией отрицания, например, умножение можно определить: a b = (-( (-a) + (-b) )) (через правила де Моргана).

Замечание 2. Это определение "неэкономно". Многие свойства могут быть выведены из других, но эта система непротиворечива и удобна для исследования.

2. Арифметические модели булевых операций

Известному немецкому математику и логику Эрнесту Шредеру пришло в голову предложить в качестве знака для обозначения ложного суждения цифру О, что, конечно, привело к обозначению истины цифрой 1. Тогда таблица истинности приобретает некий арифметический вид:

Таблица истинности:

Таблица 1

A B не A A&B AVB A=>B A<=>B

0 0 1 0 0 1 1

0 1 1 0 1 1 0

1 0 0 0 1 0 0

1 1 0 1 1 1 1

Оценивая суждения таким образом, мы находимся в двоичной системе счисления. Так как теперь имеем дело с цифрами, естественно предположить, что и логические действия можно заменить арифметическими.

Арифметические действия:

Таблица 2

щ Отрицание 1 - А

& Конъюнкция А х В или АВ

V Дизъюнкция А + В - А х В или А + В - АВ

=> Импликация 1 - А + А х В или 1 - А + АВ

<=> Эквивалентность 1 - (А - В) х (А - В) или 1-(А-В)(А-В)

Еще одно определение конъюнкции и дизъюнкции:

А&В ~ min(A,B): AVB ~ max(A,B)