СОЗДАТЕЛЬ МАТЕМАТИЧЕСКОЙ НАУКИ О МЕХАНИЗМАХ (Окончание)

(Окончание. Начало здесь ==>>)

Однажды он сказал:

• Ничего не должно быть предлагаемо (в геометрии) без доказательств.

• Нестрогие доказательства вредно действуют на умственные способности учеников, приучая их видеть там достаточную причину, где её нет.

• Новое в преподавании математики полезно только тогда, когда на опыте проверено, что оно лучше старого.

• Все арифметические правила должны быть объяснены вполне удовлетворительно и таким образом, чтобы эти объяснения могли заменить собой доказательства.

• Бессознательное заучивание различных приемов, предлагаемых в арифметике, не может принести никакой пользы, … необходимо дать понять ученику, почему при вычислении поступают так, а не иначе.

• Изустное решение арифметических задач много содействует развитию умственных способностей детей. Такие задачи представляются ежечасно в обыкновенной жизни, и дитя по необходимости приучается к решению их.

• Руководства по арифметике должны быть составлены с особым тщанием, все необходимое должно быть изложено кратко и общепонятно…

• Необходимо иметь в виду постепенный ход развития числительной способности детей.

• Концентризм как метод преподавания математики вреден, так как он разрушает систематическое изложение дидактического материала.

• Недостаточно, если ученик усвоит теорию, необходимо, чтобы ученик этой теорией овладел, а этого можно достигнуть только её приложениями к практике и решением многочисленных задач и упражнений. Ученик должен иметь возможность видеть приложение элементов высшей математики, что достигается введением преподавания элементов механики и оптики.

Рассказывают, что ...

*Фамилию учёного — по его собственному указанию — следует произносить «Чебышо́в»; в XIX веке такое произношение данной старинной дворянской фамилии (писавшейся тогда — в условиях традиционного неразличения е/ё на письме — как «Чебышевъ») было весьма распространено (предполагают, что эта фамилия по своему происхождению является кратким притяжательным прилагательным, образованным от антропонима Чебыш с ударением на окончании в косвенных падежах и на последнем слоге основы в именительном падеже).

В XX веке в связи с тенденцией к обособлению фамилий на -ов/-ёв от исходных притяжательных прилагательных и всё ещё распространённым неразличением на письме е/ё получило довольно широкое распространение ошибочное произношение «Че́бышев» (с ударением на первом слоге) — несмотря на чёткие рекомендации авторитетных источников. 4-е издание академического «Русского орфографического словаря» (2013), словарь ударений «Собственные имена в русском языке» (2001) и профильные академические издания, последовательно использующие букву ё при передаче имён и названий, фиксируют в качестве орфографической и орфоэпической нормы написание и произношение Чебышёв.

• В книге «Простая одержимость» Джон Дербишир пишет о том, как сложно ему было искать научные материалы Пафнутия Чебышёва. А сложность заключалась в том, что Дербишир насчитал 32 варианта транскрипции фамилии Чебышёв. Ведь в этой фамилии сразу несколько букв, которые неоднозначно передаются латиницей, и потому поиск по базам данных библиотек довольно затруднен. Кстати, книга американского писателя, автора научно-популярных книг посвящена теории простых чисел, в развитие которой внёс свой вклад Пафнутий Чебышёв.

*Буква ё долгое время была на письме не обязательна, поэтому фамилию великого русского математика часто произносят неправильно – с ударением на первый, а не на последний слог.

• О научных заслугах одного из величайших математиков Европы замечательно сказали его коллеги: «Труды Чебышёва носят отпечаток гениальности. Он изобрел новые методы для решения многих трудных вопросов, которые были поставлены давно и оставались нерешенными». Всё именно так: Пафнутий Львович получил фундаментальные результаты в теории чисел и теории вероятностей, построил общую теорию ортогональных многочленов, теорию равномерных приближений – все его научные заслуги трудно перечислить.

• Академик С.Н.Бернштейн писал: «Математический гений такого масштаба, как Чебышёв, не мог не оказать самого крупного влияния на дальнейший ход развития математики и должен был воздействовать в большей или меньшей степени на всякого математика, даже далёкого от Чебышева по своим интересам».

*Основатель петербургской научной математической школы сильно напугал парижских модельеров. Он выступал перед ними с лекцией о том, как математика может помочь в моделировании одежды и для простоты предложил считать, что человеческое тело имеет форму шара.

*В июне 1872 года в Петербургском университете отметили двадцать пять лет профессорской деятельности Чебышёва. По правилам, действующим в то время, профессор, прослуживший двадцать пять лет, освобождался от занимаемой должности. Но на этот раз Совет университета возбудил перед Министерством народного образования ходатайство, с тем, чтобы срок профессуры Чебышёва был продлён на пять лет. В итоге указанных хлопот Чебышев окончательно вышел в отставку только в 1882 году.

*В 1890 году президент Франции вручил Чебышёву орден Почётного легиона. По этому поводу математик Шарль Эрмит писал Чебышёву:

«Мой дорогой собрат и друг!

Я позволил себе большую вольность в отношении вас, взяв на себя смелость, как Президент Академии наук, обратиться к Министру иностранных дел с просьбой ходатайствовать о награждении вас орденом: Командорским крестом Почётного легиона, который и был вам пожалован президентом Республики. Это отличие является лишь небольшой наградой за великие и прекрасные открытия, с которыми навсегда связано ваше имя и которые давно уже выдвинули вас в первые ряды математической науки нашей эпохи…

Все члены Академии, которым было представлено возбужденное мною ходатайство, поддержали его своей подписью и воспользовались случаем засвидетельствовать ту горячую симпатию, которую вы им внушаете. Все они присоединились ко мне, заверяя, что вы являетесь гордостью науки в России, одним из первых геометров Европы, одним из величайших геометров всех времен…

Могу ли я надеяться, мой дорогой собрат и друг, что этот знак уважения, идущий к вам из Франции, доставит вам некоторое удовольствие?

По меньшей мере прошу вас не сомневаться в моей верности воспоминаниям о нашей научной близости и в том, что я не забыл и никогда не забуду наших бесед во время вашего пребывания в Париже, когда мы говорили о столь многих предметах, далеких от Евклида…»

• Весьма остроумно Пафнутий Львович Чебышёв вычислил расстояние между Москвой и Санкт-Петербургом. Нужно определить удвоенную разность широт Москвы и Санкт-Петербурга и разность их долгот. То из этих чисел, которое больше, умножить на 7, то, что меньше на 3. Потом надо сложить оба числа и разделить результат на 8. Получится расстояние между Москвой и Петербургом в верстах.

*Задолго до физиков XX века, сделавших семинары основным полем отработки новых идей, Чебышёв начал заниматься с учениками в неформальной обстановке. При этом Чебышев никогда не ограничивался только узкими темами. Отложив в сторону мел, он отходил от доски, садился в особое кресло, предназначенное только для него, и с удовольствием погружался в обсуждение любого отвлечения, интересного для него и для его оппонентов. Во всём остальном он оставался суховатым, даже педантичным человеком.

*О широте научных интересов великого математика и механика дает представление полное собрание его сочинений в пяти томах, выпущенное в 1944-1951 годах. В первом томе собраны его работы по теории числе, во втором и третьем – труды по математическому анализу, в четвертом – по теории механизмов. В пятом можно прочесть его сочинения по другим разделам математики и механики и познакомиться с биографией ученого.

*В истории развития науки о машинах нельзя указать ни одного учёного, творчеству которого принадлежало бы столь значительное количество оригинальных механизмов. Но П. Л. Чебышёв решал не только задачи синтеза механизмов. Он на много лет раньше других учёных выводит знаменитую структурную формулу плоских механизмов, которая только по недоразумению носит название формулы Грюблера — немецкого учёного, открывшего её на 14 лет позднее Чебышева. П. Л. Чебышёв, независимо от Робертса, доказывает знаменитую теорему о существовании трёхшарнирных четырёхзвенников, описывающих одну и ту же шатунную кривую, и широко использует эту теорему для целого ряда практических задач. Научное наследство П. Л. Чебышёва в области теории механизмов содержит такое богатство идей, которое рисует облик великого математика подлинным новатором техники. Для истории математики особенно важно то, что конструирование механизмов и разработка их теории послужили П. Л. Чебышёву исходной точкой для создания нового раздела математики — теории наилучшего приближения функций многочленами.

*До Чебышёва вопросы распределения простых чисел решались экспериментально, путем наблюдений и не всегда обоснованных предположений. Таким образом французский математик Лежандр (1752–1833) установил, что в пределах первого миллиона число простых чисел, меньших п, приблизительно равно

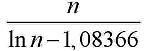
где In п означает логарифм при основании е = 2,71828… Далее Лежандр без всякого основания предположил, что указанное соотношение имеет место и при больших, чем миллион, значениях п. Французский математик Бертран (1822–1900) высказал гипотезу, что между п и 2n, где п – любое целое число, большее единицы, находится, по крайней мере, одно простое число.

Основоположником строгой теории распределения простых чисел является П. Л. Чебышёв. Его открытия в этом направлении – подлинный триумф русской математической мысли. Чебышёв строгими логическими рассуждениями доказал, что указанная выше формула Лежандра, установленная опытным путем в пределах первого миллиона, является необоснованной и неверной за пределами этого миллиона. Далее Чебышёв доказал упомянутую выше гипотезу Бертрана и тем самым установил совершенно строгое предложение, относящееся к закону распределения простых чисел в натуральном ряду. Кроме того, П. Л. Чебышёв доказал, что если π(n) – функция, выражающая число простых чисел, меньших п, то выражение

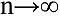
при не может иметь предела, отличного от 1.

В 1896 году, уже после смерти П. Л. Чебышёва, французский ученый Адамар и бельгийский математик Валле Пуссен, пользуясь аппаратом теории функций комплексного переменного, независимо друг от друга доказали, что

Таким образом, для достаточно больших п можно приближенно считать:

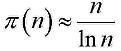
Научные открытия П. Л. Чебышёва в области теории чисел трудно переоценить, они принесли славу русской математической науке и оказали огромное влияние на научное творчество многих выдающихся ученых на родине и за рубежом.

*Особенное внимание Чебышёв уделял усовершенствованию параллелограмма Уатта - механизма, служащего для превращения кругового движения в прямолинейное. Дело заключалось в том, что этот основной для паровых двигателей и других машин механизм был весьма несовершенен и давал вместо прямолинейного движения криволинейное. Такая подмена одного движения другим вызывала вредные сопротивления, портившие и изнашивавшие машину. Семьдесят пять лет прошло со времени открытия Уатта; сам Уатт, его современники и последующие поколения инженеров пробовали бороться с этим дефектом, но, идя ощупью, путём проб, существенных результатов добиться не могли. П. Л. Чебышёв взглянул на дело с новой точки зрения и поставил вопрос так: создать механизмы, в которых криволинейное движение возможно меньше отклонялось бы от прямолинейного, и определить при этом наивыгоднейшие размеры частей машины. С помощью специально разработанного им аппарата теории функций, наименее уклоняющихся от нуля, он показал возможность решения задачи о приближённо-прямолинейном движении с любой степенью приближения к этому движению.

На основе разработанного им метода он дал ряд новых конструкций приближённо-направляющих механизмов. Некоторые из них до сих пор находят себе практическое применение в современных приборах.

*Портрет Чебышёва изображён на здании математико-механического факультета Санкт-Петербургского государственного университета, а бюст установлен на Аллее ученых МГУ.