„ВЕЛИКИЙ ГЕОМЕТР”

Аполлоний Пергский (гр. Ἀπολλώνιος ὁ Περγαῖος, лат. Apollonius Pergaios) был третьим после Евклида и Архимеда выдающимся математиком Александрийской школы. Сведения о жизни Аполлония практически отсутствуют.

     Родился он в эллинизированном малоазиатском городе Перге в Памфилии, ещё в ранней молодости присоединился к Александрийской математической школе Евклида и со временем преподавал там как признанный авторитет в геометрии и астрономии. В конце жизни на некоторое время вернулся на родину, где были открыты учебный центр и библиотека, аналогичные Александрийскому Мусейону.

      В тексте трудов Аполлония обнаружено упоминание о его сыне, которого также звали Аполлоний. Умер учёный, по-видимому, в Александрии.

Жил он около 262-190 г.г. до н.э. Математику изучал в Мусейоне у учеников Евклида.

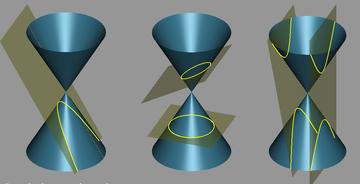
Трактат Аполлония „Конические сечения” (Коника) прославил его имя навсегда и сохранил ему в истории математики звание „Великий Геометр”. Из восьми книг этого трактата до нас дошли только три. Трактат, как это следует из названия, посвящён кривым, которые получаются при сечении конуса различно расположенными плоскостями.

    В предисловии к I книге Конических сечений Аполлоний писал Евдему Пергамскому: «Когда я посетил тебя в Пергаме, я заметил, что ты хочешь познакомиться с написанными мной ,,Коническими сечениями“. Поэтому я посылаю тебе эту первую книгу в исправленном виде; остальные я отправлю, когда сам буду ими доволен. Ведь ты, конечно, должен вспомнить, что я тебе сказал о причине, заставившей меня приняться за сочинение этих книг, а именно — о желании, выраженном математиком Навкратом, когда он гостил у меня в Алек сандрии, и о том, что когда он торопился уехать, я как можно скорее написал этот труд в восьми книгах и передал ему без всякой отделки».

    Из этих слов видно, что Аполлоний писал «Конические сечения» в Александрии. После окончания «Конических сечений» Аполлония стали называть в Александрии Великим Геометром.

Названия кривых - эллипс, парабола, гипербола - придумал Аполлоний. Ему же принадлежат термины абсцисса, ордината, аппликата, асимптота. Он обнаружил, что парабола — предельный случай эллипса, открыл асимптоты гиперболы; получил (в словесной форме) уравнение параболы; впервые изучал свойства касательных и подкасательных к коническим сечениям.

      Евклид не включил теорию конических сечений в свои «Начала», вероятно, по той причине, что античные математики считали «совершенными линиями» только прямые и окружности.

Аполлонию принадлежит требование выполнять геометрические построения только с помощью циркуля и линейки без делений.

Науку о конических сечениях Аполлоний изложил столь совершенно, что и теперь мало что можно добавить, несмотря на огромный прогресс в математике.

В своём трактате он обобщил всё сделанное до него в этом направлении. Семь первых книг трактата содержат 387 теорем со сложными доказательствами. Некоторые доказательства удалось упростить лишь спустя 2000 лет, используя методы аналитической геометрии.

       Классификация кривых у Аполлония, как и в современных учебниках, проводится алгебраически — по виду уравнения, а не из геометрических соображений. Более того, Аполлоний строго доказывает, что вид уравнения не зависит от выбора опорной системы координат; в качестве таковой выступают, как правило, произвольный диаметр кривой и касательная в одном из концов диаметра, но Аполлоний рассматривает и другие косоугольные системы координат (например, для гиперболы — пара асимптот).

  В этом труде  выясняются свойства особых точек и линий, связанных с исследуемой кривой: фокусов, асимптот, полюсов и поляр, перечисляются их свойства, доказывается, что конические сечения могут пересекаться не более чем в 4 точках, поясняется, как строить касательные к этим кривым, определяются площади сегментов. 

        Аполлоний доказывал теоремы о кривых 2-го порядка методом, который состоял в отнесении кривой к какому-либо её диаметру и к сопряжённым с ним хордам, и предвосхитил созданный в XVII в. метод координат. Все соотношения Аполлоний рассматривал как отношения равновеликости между некоторыми площадями.

В отличие от предшественников Аполлония, которые рассматривали только плоские сечения прямых круговых конусов, конические сечения, которые рассматривал Аполлоний, высекаются также из наклонных круговых конусов, и, помимо сечений одной полости конической поверхности, он рассматривал сечения обеих полостей этой поверхности.

         Аполлоний был не только математиком, но и астрономом. Он изучал движение Луны. Его прозвище „Эпсилон” происходит от серповидной формы Луны, похожей на греческую букву эпсилон. Аполлоний переработал астрономическую модель Евдокса, введя эпициклы и эксцентрики для объяснения неравномерности движения планет. Эту теорию позднее развили Гиппарх и Птолемей. Один из астрономических трактатов Аполлония цитируется в «Алмагесте» Птолемея.

    Он изучал спиральные линии, занимался геометрической оптикой.

Сочинения Аполлония переводили и изучали такие учёные как Виет, Галилей, Ферма, Гильберт. Виет перевёл трактат „О касании”, в котором рассмотрена знаменитая задача Аполлония о построении окружности, касающейся трёх данных окружностей.

Теперь мы имеем достаточно простые решения этой задачи, но во времена Аполлония эта задача была чрезвычайно трудной. У самого Аполлония решение столь громоздко, что занимает около 25 печатных страниц.

       Вслед за Архимедом, Аполлоний занимался усовершенствованием системы счисления. Значительно облегчил умножение больших чисел в греческой нумерации, разбивая десятичные разряды на классы (по четыре).

По мнению Д.Гильберта, Аполлоний был одним из тех математиков древности, которые стремились освободиться от влияния платоновской философии. Это следует из того, что в работе, посвященной основам геометрии, Аполлоний пытался найти связь между математическими понятиями и окружающей действительностью.

      Аполлоний развивал геометрию в духе Евклида, но продвинулся значительно дальше него. Книга «Конические сечения» оказала огромное влияние на творчество последующих математиков, включая Ферма, Декарта, Ньютона, Лагранжа и многих других. Многие теоремы Аполлония, особенно о максимумах, эволютах, нормалях вошли в современные учебники по дифференциальной геометрии конических сечений.

         Каким образом Аполлоний, не владея математическим анализом, сумел сделать свои открытия, неясно. Возможно, у него, как у Архимеда, был некий метод бесконечно малых, который он использовал в эвристических целях, чтобы затем передоказать результат каноническими средствами античной геометрии.

        Ван дер Варден пишет: «Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книгу и трудно понимать; рассуждения его элегантны и кристально ясны, но что его привело именно к таким рассуждениям, а не к иным каким-нибудь, — об этом можно лишь догадываться».

До открытий Кеплера и Ньютона теория Аполлония практически применялась в основном для решения кубических уравнений, а также в оптике зеркал. Когда обнаружилось, что орбита материальной частицы в задаче двух тел есть одно из конических сечений, интерес к данным кривым резко возрос, и труды Аполлония были продолжены на новом математическом уровне.

Как „чистый” геометр Аполлоний не имел себе равных вплоть до Якоба Штейнера, жившего в 19-ом веке.

Геометрия конических сечений достигла высокой степени совершенства благодаря Аполлонию и его последователям. Она оказалась чрез¬вычайно важной в небесной механике. Если бы древнегреческие геометры не предшествовали Кеплеру, то вряд ли Ньютону удалось бы установить закон всемирного тяготения, опирающийся на тщательные вычисления планетных орбит, проделанные Кеплером.

После Аполлония в Древней Греции не было крупных открытий в области геометрии. Причиной тому были войны, разорения, распад античного общества. Труды Архимеда и Аполлония считались слишком трудными, их не читали, часть из них была вообще утеряна. Были причины тому и в самой математике: трудность и громоздкость геометрической алгебры, отсутствие математической символики, резкое разделение арифметики и геометрии.

Всё же, хотя и замедленно, развитие математики в это время продолжалось. Вопросами геометрии и тригонометрии занимались Гиппарх, Менелай, Папп, новая алгебра зарождалась в работах Диофанта. Эти новые ростки греческой математики развития не получили: в 5-ом веке прекратила своё существование Западная Римская империя и вместе с ней пришла в упадок вся античная культура.

Со смертью Аполлония кончается плеяда великих математиков античного мира. Лишь в 17-ом веке в геометрии появляются существенно новые идеи и методы.

В честь Аполлония назван кратер на Луне.

Задача Аполлония

Построить окружность, касающуюся трёх данных окружностей.

• Греки немало заимствовали из культуры хеттов, в частности, культ хеттского бога-громовержца Завайи, которого они стали называть Зевсом (Zeus), бога Солнца Апулунаша и его сестры-близнеца богини Луны Артиму, которых они называли Аполлоном (Apollo) и Артемидой (Artemis). Предки славян и литовцев слова перу наш и пергунаш принесли в Европу, где они превратились в имена богов-громовержцев Перуна и Пяркунаса.

• Александрия — город и порт при впадении Нила в Средиземное море — была основана Александром Македонским после завоевания им Египта. Ещё при Александре этот город был столицей Египта, а после распада империи Александра стал резиденцией царей Египта из династии Птолемеев, основанной военачальником Александра Македонского Птолемеем Лагом.

      Основным научным учреждением Александрии был Мусейон (Mou seion) — храм муз. Большинство муз были покровительницами различ ных искусств, но две музы — муза истории Клио и муза астрономии Ура ния — были покровительницами гуманитарных и точных наук. От ла тинского названия Мусейона (Museum) произошло слово музей.

Мусейон представлял собой академию наук с университетом и богатой библиотекой рукописей. Основателем Мусейона был Евклид.

     Наиболее крупных ученых Мусейона называли первыми буквами греческого алфавита. Второй буквой — Бета — называли Эратосфена, пятой буквой — Эпсилон — Аполлония. Очевидно, что первой буквой — Альфа — называли Евклида, а третьей буквой — Гамма — Архимеда. Четвертой буквой — Дельта, — по-видимому, называли Конона — рано умершего талантливого ученого, которому Архимед посылал свои сочинения.

        Это была первая в грекоязычном мире государственная академия, с богатейшей библиотекой (ядром которой послужила библиотека Аристотеля), которая к I веку до н. э. насчитывала 70000 томов. Учёные Александрии объединили вычислительную мощь и древние знания вавилонских и египетских математиков с научными моделями эллинов. В городе Пергаме был впервые изготовлен пергамент.

      Значительно продвинулись плоская и сферическая тригонометрия, статика и гидростатика, оптика, музыка и др. Эратосфен уточнил длину меридиана и изобрёл своё знаменитое «решето».

     Конон Самосский был моложе Архимеда, но умер раньше него. Конон был геометром и астрономом. Работы Конона по коническим сечениям упоминаются в IV книге Конических сечений Аполлония. Конон написал семь книг по астрономии. В некоторых из них были приведены сведения о древневавилонских наблюдениях затмений, впоследствии использованные Гиппархом и Клавдием Птолемеем.

      На основании собственных наблюдений Конон составил календарь с указанием восходов и заходов неподвижных звезд и метеорологических предсказаний. Из звезд, находящихся вне созвездий, Конон составил новое созвездие, названное им Волосами Вероники в честь жены царя Египта Птолемея III Эвергета, правившего в 222—217 гг. до н. э.

• В истории математики известны три великих геометра древности, и прежде всего — Евклид с его «Началами». Тринадцать книг Начал — основа античной математики, итог её 300-летнего развития и база для дальнейших исследований. Влияние и авторитет этой книги были огромны в течение двух тысяч лет.

Фундамент математики, описанный Евклидом, расширил другой великий учёный — Архимед, один из немногих математиков античности, которые одинаково охотно занимались и теоретической, и прикладной наукой. Он, в частности, развив метод исчерпывания, сумел вычислить площади и объёмы многочисленных фигур и тел, ранее не поддававшихся усилиям математиков.

       Последним из тройки великих был Аполлоний Пергский, автор глубокого исследования конических сечений.

• Четыре книги главного сочинения Аполлония о конических сечениях дошли до нас в греческом оригинале, три — в арабском переводе Сабита ибн Курры, а 8-я потеряна. Эдмонд Галлей подготовил образцовое издание данного труда (Оксфорд, 1710), куда включил свою попытку реконструкции VIII книги (на основании предисловия к VII книге). До Галлея аналогичную попытку предпринял Ибн ал-Хайсам.

• После Аполлония (со II века до н. э.) в античной науке начался спад. Новых глубоких идей не появляется. В 146 году до н. э. Рим захватывает Грецию, а в 31 году до н. э. — Александрию.

Среди немногочисленных достижений:

1. открытие конхоиды (Никомед);

2. известная формула Герона для площади треугольника (I век н. э.);

3. содержательное исследование сферической геометрии Менелаем Александрийским;

4. завершение геоцентрической модели мира Птолемея (II век н. э.), для чего потребовалась глубокая разработка плоской и сферической тригонометрии.

   *Необходимо отметить деятельность Паппа Александрийского (III век). Только благодаря ему до нас дошли сведения об античных учёных и их трудах. На фоне общего застоя и упадка резко выделяется гигантская фигура Диофанта — последнего из великих античных математиков, «отца алгебры».

       После III века н. э. александрийская школа просуществовала около 100 лет — приход христианства и частые смуты в империи резко снизили интерес к науке. Отдельные учёные труды ещё появляются в Афинах, но в 529 году Юстиниан закрыл Афинскую академию как рассадник язычества. Часть учёных переехала в Персию или Сирию и продолжала труды там. От них уцелевшие сокровища античного знания получили учёные стран ислама.

• Греческая математика поражает прежде всего красотой и богатством содержания. Многие учёные Нового времени отмечали, что мотивы своих открытий почерпнули у древних. Зачатки анализа заметны у Архимеда, корни алгебры — у Диофанта, аналитическая геометрия — у Аполлония и т. д.

      Но главное даже не в этом. Два достижения греческой математики далеко пережили своих творцов. Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики. Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию. В этих двух отношениях античная математика вполне современна.

• Переводы книг Аполлония Пергского издавались крайне редко, большинство переводов были по существу пересказами. На русском языке были изданы только первые 20 теорем из главного труда Аполлония «Конические сечения». Книга Розенфельда Б. А. „Аполлоний Пергский“ М.: МЦНМО, 2004, 176 с. представляет собой попытку создания научной биографии Аполлония, содержащей анализ его трудов с точки зрения современной науки.