Однофамилец формулы

Идите к де Муавру, он разбирается в этом лучше меня.

Абрахам де Муавр – британский математик французского происхождения. Ученик и помощник Исаака Ньютона, член Лондонского королевского общества, Парижской и Берлинской академий наук. Внёс значительный вклад в развитие тригонометрии и теории вероятностей. Первый, кто использовал возведение в степень бесконечных рядов.

Абрахам де Муавр (Abraham de Moivre) родился 26 мая 1667 года в Витри-ле-Франсуа (Франция), в недворянской семье врача-гугенота; частицу де перед своей фамилией он добавил по собственной инициативе (по иным сведениям – принадлежал к семейству мелкого французского дворянства). В 11 лет поступил в Протестантскую академию в Седане, где успел проучиться 4 года, после чего академия была запрещена властями (1682). Муавр продолжил образование в Сомюре (2 года). Вероятно, в это время он познакомился с теорией вероятностей по трудам Гюйгенса.

Учился у известного французского математика Ж.Озанама (1640-1717), автора пятитомного "Курса математики" и книги "Математические и физические развлечения", которой пользовались для своих работ по занимательной математике почти все позднейшие авторы.

Но в 1685 году Людовик XIV официально отменил Нантский эдикт – закон, даровавший французским протестантам-гугенотам вероисповедные права. Возобновились притеснения протестантов, а сам Муавр попал в тюрьму. Подробности его заключения неизвестны, но, так или иначе, он вынужден был покинуть родину.

Муавр переселяется в Англию, где работает в качестве гувернёра, зарабатывает на жизнь частным преподаванием и шахматной игрой. Вскоре Муавр стал известен как талантливый математик. Однако как иностранец не имел никаких шансов на кафедру в английском учебном заведении. Религиозная дискриминация сменилась национальной. Был в дружеских отношениях с Э.Галлеем, а через него – с И.Ньютоном. Незадолго до его приезда вышла книга Ньютона «Математические начала натуральной философии» в трёх томах. Она так увлекла Муавра, что он разобрал её по листам и постоянно носил с собой очередную порцию для чтения, чтобы не терять времени при переездах от одного ученика к другому.

Ньютон чрезвычайно высоко ценил Муавра. Если верить сплетням той поры, Ньютон выпроваживал посетителей, досаждавших ему мелкими делами математического характера, с помощью следующей фразы: «Идите к де Муавру, он разбирается в этом лучше меня». Муавр также постоянно помогал Ньютону в издании и редактировании трудов (особенно «Оптики»).

Всю оставшуюся жизнь Муавр прожил в Англии, писал свои работы по-английски.

В своих работах Муавр опирался на "Алгебру" Джона Валлиса (1685) и "Начала" И.Ньютона (1687). Занимался флюксиями Ньютона, исследовал степенные ряды, первый стал использовать возведение в степень бесконечных рядов. Муавр также установил связь между рекуррентными последовательностями и разностными уравнениями. Внёс вклад в теорию решения однородных линейных разностных уравнений с постоянными коэффициентами. Занимался комбинаторными задачами и задачами теории вероятностей.

В 1695 году был опубликован первый труд де Муавра «Метод флюксий». В 30 лет Абрахама де Муавра избрали членом Лoндонского королевского общества. В качестве одного из ближайших друзей Ньютона Муавр по его поручению и от его имени в 1710 году участвовал в комиссии, разбиравшей приоритетный спор между Ньютоном и Лейбницем.

В 1718 году де Муавр опубликовал свой главный труд по теории вероятностей: «The Doctrine of Chances: A method of calculating the probabilities of events in play». Книга вызвала большой интерес и выдержала 3 издания.

В 1722 году он опубликовал открытое пятнадцатью годами ранее правило для возведения в степень комплексных чисел, а так же для извлечения корней из них. Это правило известно нам, как формула Муавра, современная запись которой принадлежит Леонарду Эйлеру:

для комплексного числа

верно, что

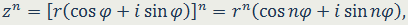
аналогично,

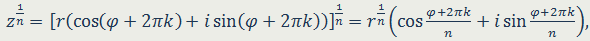
где

При целых n по этой формуле легко выразить sin nφ и cos nφ через sin φ и cos φ. Из этой знаменитой формулы Муавра можно получить формулы для вычисления корней n - ой степени из комплексных чисел.

В 1730 году появилась формула Стирлинга. Джеймсу Стирлингу и Абрахаму де Муавру принадлежит асимптотическое представление факториала. Занимаясь комбинаторным исчислением и вопросами теории вероятностей, в которых применяется ассимптоматическое число n! обозначающее произведение натуральных чисел от 1 до n. Число n! быстро растёт при увеличении n. Уже 10! равно 3 628 800. Расчёт становится трудоёмким. Де Муавр нашёл удобный способ расчёта приблизительной величины п!

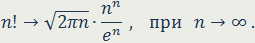
Эта формула теперь носит имя Джеймса Стирлинга.

Настоящее призвание Муавра – теория вероятностей. Тут он достиг результатов, которые поставили его имя в один ряд с такими титанами этой теории, как Паскаль, Лаплас. В 1733 г. Муавр доказал, что при большом числе испытаний функция нормального распределения вероятности является приближением биноминального закона ( распределение Бернулли).

Среди учёных, благодоря которым на колокообразную кривую – закон случайного распределения ошибок измерения – обратили внимание, реже всех воздаётся по заслугам именно её первоотктывателю Муавру, который совершил своё открытие в 1733 году, когда ему было за шестьдесят. До появления второго издания его книги "Об измерении случайности" об этом никто не знал. Де Муавр пришёл к искомой форме кривой, когда пытался аппроксимировать числа, заполняющие треугольник Паскаля. Сегодня эту кривую называют обычно нормальным распределением или Гауссовой кривой. Кривая демонстрирует, что в том случае, когда вы делаете много замеров, большинство их результатов будут примыкать к среднему значению, что изображается в виде пика.

К числу основных правил теории вероятностей причисляется теорема Муавра–Лапласа, содержащаяся во всех учебниках по теории вероятностей. Муавр внёс большой вклад в теорию вероятностей. Он провёл вероятностное исследование азартных игр и ряда статистических данных по народонаселению. Кроме нормального, он использовал равномерное распределение. Но большинство результатов де Муавра были вскоре перекрыты и обобщены трудами Лапласа. Степень возможного влияния де Муавра на Лапласа неизвестна.

Муавр был членом Лондонского Королевского общества (1697), иностранным членом Берлинской и Парижской Академий наук (1754). Какая ирония: француз по национальности, родившийся во Франции и …. иностранный член своей национальной академии.

Имя Муавра носят следующие математические объекты:

• формула Муавра,

• теорема Муавра–Лапласа.

По легенде, Муавр точно предсказал день собственной смерти. Обнаружив, что продолжительность его сна стала увеличиваться в арифметической прогрессии в сутки на 15 минут, он легко вычислил, когда она достигнет 24 часов, и, как всегда, не ошибся.

Умер А. де Муавр 27 ноября 1754 г. в Лондоне и был похоронен в Сен-Мартен-на-полях (позже его останки были перемещены).

Несколько важных работ де Муавра были опубликованы посмертно.

В его честь назван астероид (28729) Moivre.