Лидер математиков Франции во второй половине XIX века - Статьи об истории

Шарль Эрмит (Charles Hermite) родился 24 декабря 1822 г в Дьёзе (Лотарингия). Он был шестым сыном Фердинанда Эрмита и Мадлен Lallemand. Отец Эрмита был инженером в соляной шахте. К тому времени, когда Шарлю исполнилось семь лет, семья была вынуждена переехать в Нанси, другой город на северо-востоке Франции, так как их семейный бизнес был перенесён туда.

У Шарля был дефект правой ноги, что создавало трудности при ходьбе. Воспитывался он сначала в Нансийском коллеже, а затем в Лицее Генриха IV в Париже. В 1841 г. Эрмит поступил в лицей Людовика Великого. Будучи ещё школьником, самостоятельно доказал невозможность решения в радикалах уравнения пятой степени. Заметим, что работа Абеля о невозможности решения в радикалах общего уравнения 5-й степени была опубликована на немецком языке в Журнале Крелля, а на французском имелось лишь краткое изложение её. Эрмит доказал теорему Абеля своим способом.

В 1842 г. поступил в Политехническую школу, где на его способности обратили внимание Э. Каталан и Ж. Лиувиль.

В январе 1842 г. Эрмит по совету профессора Политехнической школы Ж. Лиувилля послал письмо берлинскому профессору К.-Г. Якоби с сообщением о своих исследованиях. История повторилась. За 16 лет до этого К.-Г. Якоби, в то время приватдоцент Кёнигсбергского университета, написал письмо прославленному французскому учёному А.-М. Лежандру о своих обобщениях теории преобразования эллиптических функций. Письмо Якоби к Лежандру начиналось словами: «Милостивый государь, один молодой геометр

осмеливается представить Вам несколько открытий, сделанных им в теории эллиптических функций, к которым он был приведен внимательным изучением Ваших прекрасных работ. Именно Вам, милостивый государь, эта блестящая часть Анализа обязана той высокой степенью совершенства, какой она достигла, и лишь идя по стопам столь великого мастера, геометры смогут развить её далее тех границ, в которых она находится до сих пор. Таким образом, Вам я обязан предложить то, что следует далее, как свидетельство восхищения и преданности»

Как отметил Дарбу, похвалы, воздаваемые молодым автором письма знаменитому Лежандру, были вполне тем заслужены: «В частных открытиях Фаньяно и Ландена, в гениальном интегрировании Эйлера Лежандр сумел распознать первые черты важной ветви Анализа, и несмотря на равнодушие, с каким встречали все его труды соотечественники, он не прекращал работать в течение почти пятидесяти лет над созданием теории, охватывающей все интегралы, в которые входит одна и та же иррациональность, а именно — квадратный корень из полинома четвертой степени. И именно в тот самый момент, когда Лежандр только что сумел систематизировать свои

результаты и начал публикацию большого трактата по теории эллиптических функций, открытия Якоби, за которыми последовали открытия Н. Абеля, его знаменитого современника и соперника, должны были в корне преобразовать воздвигнутое Лежандром здание и внести элементы, предназначенные для обновления всего Математического анализа.

С того времени Якоби сделался одним из знаменитых математиков. Благодаря бессмертным трудам Якоби и Абеля не только достигла более высокой ступени развития теория эллиптических функций, но родилась и новая теория, источником которой была теорема Абеля, названная Лежандром monumentum aere perennius (памятник прочнее бронзы). Эта теория связала изучение эллиптических функций с исследованием основных трансцендентных, полученных с помощью интегрирования некоторых алгебраических дифференциалов.

Эрмит распространил на абелевы функции теоремы, доказанные Абелем и Якоби для эллиптических функций. То, что умели делать для уравнения с одной неизвестной в теории эллиптических функций, он сумел осуществить для уравнений с несколькими неизвестными.

Получив письмо Эрмита, Якоби ответил: «Самым искренним образом благодарю Вас за прекрасное и важное сообщение, которое Вы мне сделали, касающееся деления абелевых функций. Обнаружением этого деления Вы открыли широкое поле для новых исследований и открытий, которые дадут сильный толчок прогрессу искусства анализа». Якоби просил поблагодарить своего прославленного друга Лиувилля «за большое удовольствие, доставленное чтением мемуара молодого человека, талант которого с таким блеском проявился в самой абстрактной части науки».

После столь успешного начала можно было ждать не менее блестящего продолжения. Но тут в жизнь юноши вторглись события, на время задержавшие его научные занятия.

От рождения Эрмит прихрамывал на правую ногу и принужден был ходить с тростью. Это не помешало ему поступить в Политехническую школу, но в середине учебного года решением Министерства ему запрещено было продолжать там занятия. Лишь благодаря ходатайству политических деятелей его департамента Эрмита оставили в числе студентов, но с условием, что по окончании Школы он не станет претендовать на какое бы то ни было назначение на государственную службу.

При таком условии пребывание в Школе теряло всякий смысл, и Эрмит, покинув её в конце первого учебного года, остался в Париже и начал готовиться к экзаменам на степень бакалавра. Одновременно он продолжал работу в избранной им области математики — теории эллиптических функций и теории чисел.

Две его статьи были представлены Парижской академии наук.

Один из учеников Эрмита, Поль Пенлеве, писал: «Начиная с первых работ проявляется главное свойство Эрмита — глубина. Он никогда не рассеивался в исследованиях поверхностных и туманных. Каждый вопрос представал перед ним всегда в исключительно точной форме: он проникал в его глубоко скрытые тайны, он вносил туда такой свет, что и все другие вопросы подобного рода оказывались сразу решены».

В программу экзаменов на степень бакалавра входил древнегреческий язык, который Эрмит стал изучать совместно с Александром Бертраном, читая с ним Гомера.

Эрмит, с его обычно доброжелательным отношением к людям, далеко не всегда одобрял действия Бертрана. Между ними случались и ссоры. Однажды примирение состоялось только благодаря вмешательству С. В. Ковалевской, жившей в это время в Париже. Из переписки Эрмита с Дю Буа-

Реймоном видно, что, высоко ценя Бертрана как учёного, Эрмит отрицательно относился к некоторым его человеческим проявлениям.

Вынужденный уход из Политехнической школы и подготовка к экзаменам, конечно, задержали на некоторое время научные занятия Эрмита. Но уже в августе 1844 г. он послал Якоби письмо, содержавшее новые результаты по теории эллиптических функций. В начале 1847 г. он отправляет еще четыре письма к Якоби, излагая в них основные идеи своих будущих исследований, и не только своих собственных, но и тех, которыми занимались впоследствии многие его ученики.

 Осенью 1845 г. состоялось знакомство Эрмита с крупнейшим французским математиком Огюстеном Коши. В это время Коши начал публиковать серию статей о перестановках и их приложениях к разным вопросам.

Несмотря на научный авторитет, Коши вначале не вызвал в молодом Эрмите особого расположения. Ведь именно он не дал отзыва о работах Абеля и Галуа, о чём неоднократно слышал Эрмит от Ришара. Может быть, по этой причине при первой встрече он не рассказал Коши, в чём точно состоит его метод. Но впоследствии они сблизились.

Итак, в 1845 г., ещё не окончив высшего учебного заведения, Эрмит уже получил важные научные результаты и установил дружеские отношения с тремя крупнейшими математиками — Коши, Лиувиллем, Якоби. Лишь 7 июня

1847 г. он сдал экзамены на степень бакалавра литературы, а в июле того же года — на степень бакалавра математических наук. Последний экзамен принимала комиссия, состоявшая из его прежнего учителя физики Депре, известного математика Ш. Штурма и Жозефа Бертрана, который к этому времени уже преподавал на Факультете наук. В июле 1848 г. Эрмит становится экзаменатором по приёму в Политехническую школу, а с 12 декабря

1848 г. — еще и репетитором по математическому анализу.

В 1848 г., поступив на службу, Эрмит сделал предложение сестре Александра и Жозефа — Луизе Бертран, которое было принято. Супруги прожили вместе более 50 лет, жена ненамного пережила Эрмита. У них были две дочери: старшая вышла замуж за Жоржа Форестье, одного из выдающихся французских инженеров, а младшая дочь стала женой математика Эмиля Пикара, одного из любимых учеников отца. Впоследствии Пикар сменил Эрмита на его кафедре в Сорбонне.

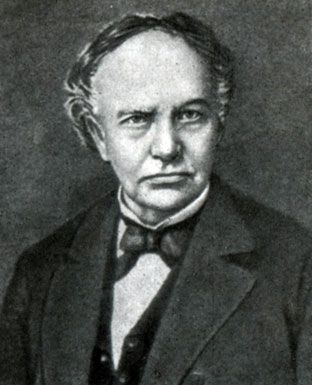
Каждое лето Эрмит, обычно в сопровождении жены, ездил по стране для приёма экзаменов в Политехническую школу. В свободное время он посещал оперные спектакли со своими коллегами-экзаменаторами — Ж. Серре и О. Бонне.

Не получив никакого музыкального образования, Эрмит унаследовал от отца прекрасный слух и превосходную музыкальную память, легко подбирал на фортепьяно услышанные мотивы. В отличие от музыкального искусства

живопись и скульптура оставляли его равнодушным.

Эрмит продолжал исполнять скромные обязанности экзаменатора и репетитора, а его товарищи уже успели получить назначения на должности профессоров Сорбонны, Политехнической школы, Коллеж де Франс. Правда,

в 1848 г. оказалось вакантным место в Коллеж де Франс, и в течение двух лет Эрмит читал там математику, пока в штат не был взят Лиувилль.

В результате этих лекций Эрмит написал статью, где изложил теорию двоякопериодических функций с новой, оригинальной точки зрения.

Лишь в 1862 г. по инициативе знаменитого Луи Пастера основоположника современной микробиологии, при Нормальной школе была образована новая кафедра, которую в течение семи лет занимал Эрмит. Одним из первых его учеников в Нормальной школе был Гастон Дарбу.

Прежде чем стать профессором, Эрмит 40 голосами из 48 был избран членом Парижской академии наук. В 1889 г. он был вице-президентом Академии наук, в 1890 г. — президентом.

В 1869 г. Эрмит, которому уже исполнилось 46 лет, сменил вышедшего в отставку профессора Ж. Дюамеля в Нормальной школе и Сорбонне. 11 ноября 1869 г. он был назначен также профессором математического анализа в Политехнической школе. Кафедру в Политехнической школе он занимал до 1876 г., после чего преподавал только в Сорбонне, где с 1875 г. читал интегральное исчисление, теорию функций, теорию эллиптических функций, часто сокрушаясь по поводу того, что из регулярного преподавания исключена теория чисел.

Эрмит был прирожденным преподавателем, воспитателем молодых талантов. Не случайно среди его слушателей оказалось столько будущих знаменитых учёных.

Портрет Эрмита-преподавателя останется незавершенным, если хоть несколько слов не будет сказано о его учебных курсах. Изданные печатным или литографским способом, они распространялись по всему миру и оказали огромное влияние на несколько поколений математиков.

Во второй половине 1856 года его здоровье ухудшилось, он заболел оспой.

После смерти в 1857 году О. Коши Эрмит стал ведущим математиком Франции. С 1869 года он - профессор Парижского университета. Членом Лондонского королевского общества Эрмит был с 1873 года.

Около 200 работ Эрмита относятся к теории функций, решению алгебраических и трансцендентных уравнений, теории рядов, теории чисел, механике и др.

Но основные его работы относятся к теории эллиптических функций и её приложениям.

Трансценде́нтное число́ — число, не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Таким образом, трансцендентные числа противопоставляются алгебраическим числам. Трансцендентными числами являются: число π (3, 14159...); десятичный логарифм любого целого числа, не изображаемого единицей с нулями. Существование трансцендентных чисел впервые установил Ж. Лиувилль (1844). Отправной точкой для рассуждений Лиувилля послужила его теорема, согласно которой порядок приближения рациональной дроби с данным знаменателем к данному иррациональному алгебраическому числу не может быть произвольно высоким. Ещё одно доказательство существования трансцендентных чисел дал Г. Кантор (1874), который заметил, что множество всех алгебраических чисел счётно (то есть все алгебраические числа могут быть перенумерованы), тогда как множество всех действительных чисел несчётно.

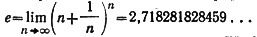
Эрмитом была доказана трансцендентность неперова числа (основания натурального логарифма) (1873). Используя метод, аналогичный методу Эрмита, К. Линдеман в 1882 г. доказал трансцендентность числа π. Этим самым была доказана и невозможность решения с помощью циркуля и линейки задачи квадратуры круга.

Известие о доказательстве Линдемана Эрмит воспринял с огромным удовлетворением. Он пишет Дюбуа-Раймону: «Вы понимаете, с каким интересом я встретил прекрасное открытие г. Линдемана, который любезно сообщил мне о нём и написал о своём методе письмо, прохождение которого г. Бертран не задержал и которое появится в отчете о последнем заседании. Для меня чрезвычайно большая радость, что я мог содействовать своими прежними исследованиями результату, который намного их превосходит и заполняет в анализе колоссальный пробел. И разве не доказывает это блестящим образом, что германцы и кельты — одно и сражаются на поле науки одним и тем же оружием!»

В различных разделах математики именем Эрмита названы полиномы, формулы, функции, матрицы, ядра, операторы, структура, тензор, пространства, многообразие. Эрмит называл создателей теории инвариантов, то есть А. Кэли, Д.Сильвестра и себя, "троицей инвариантов". Его именем назван кратер на Луне.

Он был убеждён, что числа и аналитические функции не являются плодами человеческого разума, а реально существуют вне нас и независимо от нас, подобно предметам реального мира, и что математики открывают их и исследуют так, как это делают, например, физики, химики или биологи. Поэтому нет ничего удивительного, что в одном из писем нидерландскому математику Стильтьесу, его другу, Эрмит писал: „Я с отвращением отвергаю это, достойное сожаления, болото функций без производных". Дело в том, что исследования основ анализа привели к необходимости заниматься некоторыми функциями с неожиданными и странными по тем временам свойствами. Пуанкаре неодобрительно отзывается о новых функциях, не имеющих практических применений. Как видно из высказываний Эрмита, он был тоже ярым противником исследования этих функций. На самом деле эти исследования привели к возникновению в середине XIX века новой отрасли математики, которая ныне известна как теория функций действительных переменных.

Эрмит обладал удивительным талантом преподавателя. Влияние Эрмита на развитие математики второй половины XIX—первой половины XX веков бесспорно. Достаточно напомнить, что почти все крупные французские математики этого периода были его учениками и среди них —

Анри Пуанкаре, Эмиль Пикар, Гастон Дарбу, Поль Аппель, Эмиль Борель, Камилл Жордан, Поль Пенлеве и другие знаменитые математики.

Помимо математических работ, перу Эрмита принадлежит немало биографических очерков о математиках, речей, предисловий к различным изданиям, высказываний по вопросам истории науки. Прекрасный исторический обзор преподавания математики в Сорбонне Эрмит дал в своей речи на открытии «Новой Сорбонны».

Убежденный интернационалист в науке, Эрмит стремился к установлению контактов с учёными разных стран, в том числе и России. Нередко общение на чисто научной основе приобретало дружеский характер. Именно так сложились его отношения с П. Л. Чебышевым, Е. И. Золотаревым, А. Н. Коркиным, С, В. Ковалевской, А. А. Марковым и др. Русские учёные высоко ценили научные заслуги Эрмита и не менее — его личные качества. Он оказал большое влияние на творчество Коркина и Золотарева, частично и на исследования Чебышева, но и сам испытал на себе влияние последнего. Эрмит пропагандировал идеи и результаты русских математиков во Франции, сообщая о них в своих лекциях в Сорбонне и Политехнической школе и в своих печатных курсах. А. А. Марков, в свою очередь, усовершенствовал доказательство Эрмита трансцендентности числа е.

В 1857 г. он был избран членом-корреспондентом Петербургской академии наук по представлению, составленному Чебышевым и подписанному, кроме него, В. Я. Буняковским, Д. М. Перевощиковым и Б. С. Якоби. В 1895 г. по представлению А. А. Маркова и Н. Я. Сонина Эрмит был избран почётным членом Петербургской академии наук. А задолго до этого он по представлению профессора К. А. Поссе был избран почётным членом Петербургского университета.

В 1900 г. в Париже проходил Всемирный конгресс математиков. Почётным президентом его участники единодушно избрали Шарля Эрмита, отсутствовавшего по болезни, и послали ему приветственную телеграмму:

«Международный конгресс математиков выражает своё восхищение и почтительную симпатию знаменитому Геометру, который составляет славу своей страны и всего научного мира как благодаря своему таланту, так и благодаря своему характеру. Математики всех стран единодушно шлют господину Эрмиту самые искренние пожелания здоровья и счастья.»

Получив это теплое послание, Эрмит тотчас же ответил президенту Конгресса Анри Пуанкаре: «Будьте добры передать членам Конгресса мою благодарность и выразить им, сколь глубоко я тронут свидетельством их симпатии. Это свидетельство пришло в конце моей карьеры. Оно является для меня самой высшей и лучшей наградой. Оно наполняет меня радостью и гордостью, соединяя в себе дружеские и научные связи. Я отвечаю на него всем сердцем, благодарю за него друзей, адресую пожелания успеха Конгрессу, желаю, чтобы он способствовал их трудам и внёс вклад в прекрасное будущее Анализа на новых путях, которые он открыл. Шарль Эрмит»

В жизни Эрмит отличался большой скромностью. Награждён орденом Почётного легиона (1892).

Умер Шарль Эрмит 14 января 1901 года в Париже. Считается, что в последние годы Эрмит страдал от приступов астмы. Однако фактическая причина его смерти не известна.

Парижская академия наук вынесла решение об издании собрания сочинений Эрмита, так как его работы были рассеяны в большом числе научных журналов. Туда же была включена и часть писем Эрмита. Сочинения Эрмита составили 4 тома.

Рассказывают, что

Жак Адамар рассказывал случай из времён его юности, когда он боялся пострадать из-за родства с женой полковника Дрейфуса.  Дело Дрейфуса до предела накалило страсти во Франции. Общество разделилось на сторонников Дрейфуса и его противников. К последним относился и Эрмит, которому юный Адамар должен был сдавать экзамены перед защитой диссертации. Адамар ждал этого мгновения со страхом. Можно представить его состояние, когда старик Эрмит вдруг сказал: «Мосье Адамар, вы предатель». Адамар пробормотал что-то нечленораздельное, а Эрмит продолжал: «Вы покинули геометрию ради анализа».

 Не заботясь о своем приоритете, Эрмит постоянно делился своими идеями, соображениями, уже начатыми исследованиями, руководствуясь единственным принципом, достойным истинного учёного: важен лишь итог — открытие, а кому оно принадлежит — второстепенно. Не раз Эрмит был инициатором исследований, удовольствие продолжать которые, равно как и получать результаты, предоставлял другим ученым. Так было с доказательством трансцендентности числа  π и доказательством невозможности решения задачи квадратуры круга с помощью циркуля и линейки. Метод принадлежал Эрмиту, а слава досталась применившему этот метод к доказательству трансцендентности числа π Линдеману. Так случилось и  с теорией квадратичных форм и геометрией чисел Г. Минковского. Эрмит первым поздравлял победителя, искренне радуясь его успеху. Он всегда стремился привлечь энтузиастов в излюбленные области своих трудов — в теорию  эллиптических и аналитических функций, теорию квадратичных форм.

Представление об облике молодого Эрмита даёт карандашный портрет, помещённый в первом томе его «Сочинений»: волнистые волосы, высокий лоб, умные ласковые глаза, лицо доброжелательное и приветливое.

Давид Гильберт вспоминал, что в первый его приезд в Париж Эрмит «не только продемонстрировал свою знаменитую вежливость, без промедления нанеся ответный визит, но также был столь добр, что предложил провести со мной свободное от лекций утро».

После нового доказательства Гильбертом трансцендентности чисел е и π Герман Минковский писал ему: «Я живо представляю себе оживление Эрмита, вызванное чтением твоей статьи. Насколько я знаю старика, я не удивлюсь, если в ближайшем будущем он сообщит тебе о своей радости, что он способен ещё испытывать наслаждение от такой радости»

В начале января 1882 г. в Париж приехала С. В. Ковалевская (1850—1891), чтобы встретиться там с мужем, В. О. Ковалевским (1842—1883). Ковалевская знакомится с французскими математиками — III. Эрмитом, А. Пуанкаре, Э. Пикаром, П. Аппелем, Г. Дарбу, Ж. Таннери. В первые же дни своего пребывания во Франции она встретилась с Эрмитом, и вскоре они стали друзьями. Обычно редко делившийся с посторонним положением своих семейных дел, Эрмит посвятил Ковалевскую в подробности взаимоотношений между своими родственниками. Письма Эрмита к Ковалевской хранятся в архиве Миттаг-Леффлера в Швеции.

Ратуя за участие женщин в научном творчестве, Эрмит сравнивает Ковалевскую с французской женщиной- математиком и философом Софи Жермен (1776—1831): «Вы, сударыня, больше будете способствовать успеху этого дела (деятельности женщин в науке), чем м-ль Софи Жермен, как благодаря превосходству Вашего таланта, так и потому, что Вы появились в благоприятную эпоху».