Забытые имена. Женщины-математики /Продолжение/

(Продолжение. Начало здесь ==>>)

В отличие от других женщин-математиков, Мария Аньези не отличалась бурной биографией. Она родилась 16 мая 1718 года в Милане, была скромной и тихой, как голубка, возможно, стала монахиней, жила в бедности и вела благочестивую жизнь, хотя из-под её пера всё же вышло нечто неслыханное, — и умерла, как птица.

Добродетели Марии Аньези были воспеты лишь после её смерти. Если развернуть атлас Венеры, то увидим кратер, названный её именем, — это общепринятая дань уважения великим учёным, которые, по мнению потомков, достигли вершин славы.

Отец Марии, Пьетро Аньези, был не университетским преподавателем, как считалось ранее, а разбогатевшим торговцем шёлками. Он оставил после себя 21 ребенка, что сегодня кажется совершенно неслыханным. До зрелого возраста дожили лишь немногие из его детей, что в те времена было обычным делом. Мария была старшей дочерью, и забота о братьях и сёстрах легла на её плечи.

Одна из сестер Марии Гаэтаны по имени Мария Тереза Аньези обожала музыку и стала известным композитором. Ей принадлежат семь опер и множество инструментальных пьес для клавесина.

Жизнь Марии была посвящена братьям и сестрам, музыке и многочисленным приёмам в доме отца, на которых тот хвастался талантами старшей дочери-полиглота: в девять лет она уже говорила на латыни, иврите и греческом, а также на четырех современных языках; французским Мария в совершенстве овладела уже в пятилетием возрасте.

Она была вундеркиндом во всех смыслах и могла поддержать беседу на любую научную или философскую тему. В девять лет Мария уже делала переводы на латынь и выступила с речью, доказывающей ценность качественного образования для женщин (текст речи, предположительно, написали её учителя).

Неудивительно, что отец гордился такой дочерью и выставлял её на всеобщее обозрение, словно фамильную драгоценность. Следует отметить, что в Италии XVIII века подобное вовсе не порицалось: на родине Возрождения женщины не считались людьми второго сорта, уделом которых было хранить домашний очаг и рожать детей, — общество с радостью встречало талантливых женщин. В других, менее просвещенных странах, в те годы грехом для женщины считалось даже умение читать и писать, ибо возможность рождает опасность, и женщин, знавших грамоту, подстерегали искушения и соблазны. Так что эта привилегия дозволялась только женщинам, жившим в монастырях или постриженным в монахини.

Мария, однако, характер имела необщительный и довольно замкнутый, поэтому быть в центре внимания не доставляло ей удовольствия. Итогом встреч в салонах стала публикация книги «Философские суждения» в 1738 году, где Мария изложила свои идеи обо всём земном и божественном, представив их в виде 171 тезиса. Уже в те годы она проявляла свою набожность, поэтому книга также имела религиозный уклон. В «Философских суждениях» девушка, среди прочего, рассмотрела теорию приливов, выразила поддержку идей Ньютона, описала природу света и свойства определенных геометрических кривых.

21 ребенок отца Марии родился не от одной женщины — чтобы произвести на свет столь многочисленное потомство, Пьетро Аньези потребовалась помощь трех жен. Когда умерла его первая жена, у Марии, которой в то время было 20 лет, состоялся серьезный разговор с отцом. Девушка пообещала и впредь заботиться о многочисленном семействе, но в обмен на это потребовала не выставлять её на приёмах на всеобщее обозрение. Она также отказалась уходить в монастырь, но, к счастью для науки, не оставила математику. Среди ее многочисленных друзей-математиков был Якопо Франческо Риккати (1676–1754), блестящий специалист по дифференциальным уравнениям, который даже высылал Марии отредактированные рукописи, чтобы она включила их в будущую книгу «Основы анализа для итальянской молодежи».

Единственным, но объёмным математическим трактатом, принадлежащим её перу, были «Основы анализа для итальянской молодежи». Казалось, всё шло своим чередом: книга была закончена и опубликована. Мария получила широкую известность как математик, о ней услышал даже папа римский Бенедикт XIV. Узнав об удивительных способностях девушки и преисполнившись гордости за достижения итальянки, в 1750 году он присвоил ей звание профессора университета Болоньи — и имел на то полное право, так как Болонья в те годы относилась к папской области. Бенедикт получил книгу Марии Гаэтаны и остался впечатлён ею, хотя, скорее всего, ничего не понял из прочитанного. Можно только сожалеть, что Мария не занялась преподаванием — она была избрана членом Академии наук Болоньи, но стремилась к покою и духовной жизни, и её желание со временем исполнилось.

Императрица Мария Терезия Австрийская, которой была посвящена книга, пожаловала Марии кольцо с бриллиантами и хрустальную шкатулку, крышка которой была украшена драгоценными камнями.

Отец семейства Аньези скончался в 1752 году, и Мария, получив полную свободу, посвятила себя богословию. Она возглавила миланский «Пио Альберго Тривульцио» — учреждение призрения для нищих и обездоленных. Само учреждение и все его служащие также были ужасно бедны. Весьма вероятно, что Мария постриглась в монахини и отказалась от искушений материального мира, чтобы посвятить себя исключительно миру духовному и служению беднякам. Ей не хотелось быть знаменитым математиком, поэтому Мария оставила и науку. Как-то раз, уже в «Пио Альберго», её попросили прокомментировать книгу о вариационном исчислении юного и талантливого туринского ученого Жозефа Луи Лагранжа (1736–1813). Мария отказалась, объяснив это тем, что больше не уделяет внимания подобным вещам.

9 января 1799 года Мария Аньези умерла, по всей видимости, в нищете, как того и хотела, — считается, что она продала всё имущество и передала вырученные деньги приюту.

Первой математической работой Аньези было составление аннотаций и комментариев к труду маркиза Лопиталя о конических сечениях. Эта юношеская работа никогда не была опубликована. Печатное математическое наследие Марии сводится к единственной книге — «Основам анализа для итальянской молодежи», — в которой рассматриваются, главным образом, дифференциальное и интегральное исчисление. Мария написала эту книгу на тосканском диалекте итальянского языка (на этом же диалекте писал Данте), когда ей было около 20 лет, но труд был опубликован лишь в 1748 году.

Возможно, Мария изначально представляла себе эту книгу как учебник для младших братьев и сестер, но затем умерила свой пыл. Хотя больше она не написала ни одного труда, «Основ анализа» по многим причинам оказалось достаточно. Во-первых, это настоящий учебник по математике, самый ранний из всех дошедших до наших дней. Во-вторых, книга отличалась ясностью изложения: она написана настолько понятно, а разрозненные результаты представлены столь логично, что чтение этого двухтомного труда доставляет истинное удовольствие.

Создается впечатление, что автор хотела сделать «Основы анализа для итальянской молодежи» в самом деле доступными для самого широкого круга читателей. Использованные обозначения столь тщательно отобраны и современны, что, по мнению многих, труд Марии будет понятен даже современному читателю. Аньези в работе над книгой применила обозначения, введённые таким видным математиком, как Леонард Эйлер.

Третья причина, по которой труд Аньези стоит особняком, носит более глубокий характер. Европа в те годы была разделена на два лагеря: островной, то есть радикальных сторонников теорий и обозначений британского учёного Исаака Ньютона, и континентальный — лагерь сторонников Лейбница. Каждый принадлежал к тому или иному лагерю, подобно тирийцам и троянцам, магометанам и христианам или современным футбольным фанатам.

Марии удалось решить очень сложную на тот момент задачу: объединить в своей книге обе точки зрения (по сути, эквивалентные), взяв лучшее из каждой. С другой стороны, Мария сделала упор на том, что две основные операции в математическом анализе — дифференцирование и интегрирование — являются взаимно обратными, и это очень современный подход.

Книга Аньези считалась наиболее понятной и полной со времён публикации труда маркиза Лопиталя, изданного более чем 50 годами ранее. Важно и то, что труд Марии иллюстрирован гравюрами, которые делают изложение более доходчивым.

В те времена, когда искусство книгопечатания ещё только развивалось, использование гравюр в учебнике было настоящей роскошью. Публикацию оплатила семья Аньези. Мария перевезла печатные машины к себе домой, чтобы полностью контролировать процесс. Книга имела широкие поля, была отпечатана большим и легко читаемым шрифтом.

«Основы анализа для итальянской молодежи» сразу после публикации не приобрели особую известность — математический анализ в те годы не был популярен, а кроме того, научным работам, в которых не излагались новые открытия, в те годы не придавалось большого значения. Следует понимать, что Мария не ставила целью написать целый трактат, а хотела создать учебник по анализу, тщательно отобрав множество примеров. Но со временем её книга стала известной и была переведена на английский и французский языки. Французский перевод был выпущен достаточно поздно, так как редакторы дополнили оригинал рядом тригонометрических понятий, которых, по их мнению, не хватало в тексте, и оказались правы.

История английского перевода заслуживает особого рассказа. Его автором стал кембриджский преподаватель Джон Колсон, искренний ценитель труда Марии, к сожалению, плохо знавший итальянский язык. В конце первого тома была изображена и подробно рассмотрена особая кривая, которую первым описал геометр Гвидо Гранди (1671–1742). Гранди назвал свою кривую curva versoria, применив морской термин, обозначавший веревку, которая позволяла поворачивать парус.

Слово versoria происходит от латинского vertere, и Гранди провёл аналогию между этим латинским словом и выражением sinus versus (синус-верзус, или обращенный синус). Все это стало причиной ошибки в переводе. Сегодня считается, что Колсон при переводе перепутал словосочетание la versiera di Agnesi со словами la awersiera di Agnesi. Эта ошибка также была бы не слишком заметной, если бы слово awersiera не означало «ведьма» или «колдунья». В результате во всех англоязычных книгах по математике эта кривая называется «ведьма Аньези» (The witch of Agnesi). Это дьявольское название произвело фурор, и Мария Аньези, которая уже постриглась в монахини, стала известна в мире математики не только как автор «Основ анализа», но и по этому яркому и не вполне богоугодному названию кривой. Ошибка распространялась всё шире, и ход событий было уже не остановить. Одна женщина-композитор даже написала музыкальную пьесу для семи инструментов под названием The witch of Agnesi.

Несмотря на эти досадные неточности, труд Колсона, который умер много лет спустя, так и не дожив до публикации этого перевода, был крайне важен. Он взялся за работу, движимый искренним восхищением красотой книги Аньези, и даже потрудился (и совершенно напрасно) заменить обозначения Лейбница сумбурной нотацией Ньютона. Впрочем, чего ещё можно было ожидать от островного математика?

История оказалась жестокой и несправедливой. Труд Аньези занимает более 20 томов в Амброзианской библиотеке Милана, но если сегодня мы спросим какого-нибудь учёного, знакома ли ему фамилия Аньези, он если и ответит положительно, то наверняка упомянет «ведьму Аньези», а не женщину-математика и её удивительный вклад в науку.

Верзьеру Аньези рассматривали ещё Пьер Ферма (1601–1665) в 1630 году и Гвидо Гранди — в 1703-м. Эта кривая определяется как геометрическое место точек, обладающих общим свойством, которое формулируется не самым простым образом.

Рассмотрим декартову систему координат и построим в ней окружность диаметра а с центром в точке С, расположенной на вертикальной оси. Обозначим через О и Т соответственно нижнюю и верхнюю точки окружности, лежащие на оси у.

Верньера Аньези определяется следующим образом: выберем точку окружности А и проведём прямую ОА, которая пересечет в точке В прямую, образованную точками с ординатой а (эта прямая параллельна горизонтальной оси координат и проходит через точку Т).

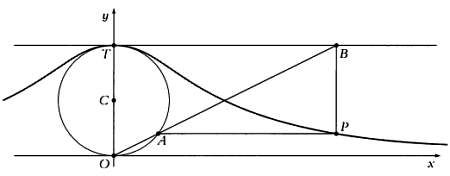
Соответствующей точкой верзьеры Аньези будет точка Р, отмеченная на иллюстрации: ее ордината равна ординате точки А, абсцисса — абсциссе точки В. Объяснить построение верзьеры Аньези сложнее, чем понять его основной принцип. Полученная кривая по своей форме в самом деле напоминает веревку, с помощью которой поворачивается парус.

Уравнение этой кривой в декартовых координатах выводится совершенно иначе, но также без особых сложностей: проведя некоторые расчёты, любой способный старшеклассник покажет, что искомое уравнение выглядит следующим образом:

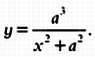
Верзьера Аньези — кубическая кривая. Если диаметр исходной окружности равен единице, то уравнение верзьеры Аньези будет особенно простым:

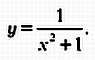
Верзьера Аньези известна прежде всего благодаря своему названию, но сегодня она редко используется в высшей математике (вместе с коноидом Плюкера и зонтиком Картана).

• Софи Жермен родилась 1 апреля 1776 года в Париже и была средней из трех сестёр в семье, которую можно назвать богатой, но не знатной. Её отцом, как считает большинство историков, был преуспевающий торговец шелками, который в итоге возглавил Банк Франции. Софи спокойно пережила сложные времена Великой французской революции, в ходе которой по той или иной причине или вовсе без причин множество людей лишилось своих постов и даже жизни.

Софи провела годы Террора, сражаясь не с Робеспьером, а с устройством мира, в котором, казалось, не было места женщине, желавшей заниматься математикой. В знатных семьях считалось хорошим тоном, если женщина немного разбиралась в науке, чтобы просто поддержать беседу. Но для женщины из буржуазной семьи стремление разбираться в науке считалось глупостью: она не должна была покидать священный мир ниток, иголок, пианино, акварелей и детей.

Доказательством этому послужит книга той эпохи под названием «Ньютонизм для дам». В одной из глав аристократическая пара обсуждает закон всемирного тяготения Ньютона. В диалоге, который можно назвать сюрреалистичным, маркиза проводит аналогию, которая привела бы самого Ньютона в ужас: «Этот закон тяготения верен и для любви — после восьми дней разлуки любовь становится в шестьдесят четыре раза сильнее».

Софи начала интересоваться математикой, когда прочла в книге Монтукля, взятой из отцовской библиотеки, о гибели Архимеда от рук римского солдата: «Оставь меня в покое и не трогай моих чертежей», — сказал Архимед солдату, который предложил мудрецу пройти с ним. Возмущенный непочтительностью Архимеда, солдат зарубил его мечом. Софи задумалась: если учёный пожертвовал жизнью ради чертежей, в них, наверное, было сокрыто нечто очень ценное. В чем же заключается ценность геометрии, сравнимая с ценностью самой жизни?Она осмеливалась читать Эйлера и Ньютона! Её близкие родственники были очень недовольны подобной экстравагантностью. Эти поступки считались недостойными женщины, которая замахнулась на то, чтобы изучать науки, предназначенные исключительно для стойкого мужского ума. Считалось, что знание математики могло ввергнуть женщину в сумасшествие, так как её скудный ум не в состоянии уместить подобные излишества. Родственники Софи перепробовали всё: так как девушка занималась математикой по ночам, они прятали её одежду, чтобы она не могла выйти из комнаты, отбирали у неё свечи, канделябры и светильники. Всё было напрасно — Софи не боялась холода, одевалась в лохмотья и тайком проносила в комнату огарки свечей.

Как и в любой долгой битве, верх одержал тот, кто был упорнее и решительнее. Так Софи Жермен стала прекрасным математиком-любителем. Мы назвали её любителем не случайно: если бы ей попался опытный наставник, который занялся бы её образованием и подсказал, какие книги следует прочесть, она вошла бы в число избранных. Софи всегда отличалась превосходным воображением, интуицией и стратегическим мышлением, и хотя порой её рассуждениям недоставало чёткости, она была способна проникнуть в суть вопросов.

В 1794 году открылись двери образцовой Политехнической школы, созданной практически с той же целью, что и военная академия США в Вест-Пойнте: её выпускниками должны были стать высококлассные специалисты, которые применили бы свои высочайшие знания математики в военных целях. Очевидно, что сколь похвальными ни были цели учреждения Политехнической школы, в их число не входило обучение женщин. Но это препятствие не казалось Софи непреодолимым. Один из её друзей по имени Антуан Огюст Леблан посещал занятия в Политехнической школе, и Софи, заручившись его согласием, читала все конспекты и учебники и могла подписывать работы его именем. Так Софи начала обучение.

Когда Леблан покинул Париж, администрация школы не заметила его отсутствия и по-прежнему высылала ему все материалы и упражнения. Софи решала домашние задания и высылала их обратно. Курс вёл Лагранж, один из самых блестящих математиков, который не переставал удивляться перемене, произошедшей с Лебланом: совершенно не способный к математике студент вдруг проявил блестящие способности, оригинальность и творческий подход.

Лагранж захотел встретиться с ним, и представьте, каково было удивление преподавателя, когда он обнаружил подлог: то был не «он», а «она». К счастью, Лагранж всегда с уважением относился к женщинам, так что он стал наставником и учителем Софи.

Итак, Софи Жермен всецело посвятила себя математике. Она так и не вышла замуж и направила всю энергию на занятия любимым делом. В частности, девушка занялась теорией чисел и теоремой Ферма, которая привлекла её внимание простой формулировкой.

Софи начала свой путь в математике, можно сказать, встав под знамена Лежандра и ещё одного известного ученого.

Еще в молодости, в 1804 году, Софи написала ни много ни мало лучшему математику мира, К.Ф. Гауссу, объяснив ему свои идеи и рассказав об открытиях, связанных с теоремой Ферма. Гаусс после публикации «Арифметических исследований» считался ведущим специалистом по теории чисел, поэтому Софи обращалась к нему в письме с особым почтением. Она подписала письмо псевдонимом Леблан — в противном случае адресат мог не принять её всерьёз. К удивлению Софи, Гаусс довольно дружелюбно ответил ей, хоть и не привёл ответов на все её вопросы. Вероятно, этих вопросов было слишком много, и прославленный учёный не нашёл достаточно времени для этого. Однако то, что показалось Гауссу интересным, он прочёл.

Обман раскрылся спустя несколько лет, когда Наполеон отправил свои армии в Германию. Софи, опасаясь, что с Гауссом что-то случится, обратилась к одному из своих друзей, генералу Пернети, который волей случая командовал войсками, расположившимися вблизи поместья Гаусса. Пернети галантно исполнил поручение и обеспечил безопасность учёного и его имущества, однако во время одного из визитов допустил оплошность, раскрыв Гауссу истинное лицо господина Леблана. Изумленный Гаусс написал Софи: он никогда не подумал бы, что автором столь глубокомысленных математических утверждений может быть женщина.

Софи Жермен всегда ассоциируется с доказательством знаменитой теоремы Ферма. Математики сразу же поняли, что Ферма в своем «чудесном доказательстве» допустил ошибку (скорее всего, он ошибся на одном весьма непростом этапе доказательства, когда используется определённый круговой многочлен — но не будем вдаваться в детали), но исправить эту ошибку и найти доказательство никак не удавалось. Привлекательность теоремы Ферма неоспорима: её может понять любой; с ней, по словам самого Ферма, связана отдельная загадка; она записывается с помощью всего нескольких математических символов; за её доказательство предлагались внушительные денежные премии и так далее. Профессиональные математики почти всегда относились к теореме Ферма с меньшим энтузиазмом, чем простые смертные. Нельзя отрицать, что эта теорема — самая известная в математике, но такие звезды, как Гаусс или, позднее, Гильберт, не уделяли ей особого внимания.

Можно сказать, что именитые учёные вели себя, словно лисица из басни «Лиса и виноград», хотя в разговоре о подобных гигантах мысли следует воздерживаться от подобных обобщений. Гаусс указывал, что доказательство теоремы Ферма не вызвало бы особого прогресса в науке, а его предполагаемые следствия были, скорее всего, не слишком важными. Кроме того, — и в этом Гаусс был совершенно прав — он сам мог сформулировать множество похожих теорем.

Как бы то ни было, доказать теорему Ферма было совсем не просто. Софи Жермен, к примеру, доказала, что при п = 5 если и существует контрпример, то он выражается колоссальной величиной — по её подсчетам, превосходящей 691053006763356095514121490614455078525. В поисках доказательства требовалось двигаться медленно и рассматривать сначала отдельные показатели степени, затем — семейства показателей.

Расскажем о принципиально новом подходе к доказательству теоремы Ферма, который применила Софи Жермен. Ранее (и позднее) предпринимались попытки доказать теорему одним и тем же способом: показать, что не существует х, у z таких, что хn + уn = zn для какого-то конкретного n. Так, Ферма доказал свою теорему для n = 4, Эйлер — для n = 3, Лежандр — для n = 5, Ламе — для n = 7 и так далее. Софи выбрала иную стратегию и попыталась определить, при каких условиях определённые значения n можно будет исключить из рассмотрения. Для этого она описала особый класс простых чисел р (сегодня они называются простыми числами Жермен). Простое число р называется простым числом Жермен, если 2р + 1 также является простым. Приведем в качестве примера простые числа Жермен, меньшие 200: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179 и 191. Еще один любопытный факт: наибольшее известное (на 2011 год) простое число Жермен равно 183027•2265440 — 1 и содержит 79911 цифр.

Частичное доказательство теоремы Ферма, полученное Софи Жермен, понять непросто даже сейчас, по прошествии более 200 лет. Результаты, полученные Софи Жермен, были приняты широкой публикой лишь в 1830 году, с публикацией «Теории чисел» Лежандра.

После наполеоновской кампании Гаусс был назначен директором Гёттингенской обсерватории и перестал уделять особое внимание теории чисел. Он занялся другими темами и прекратил переписку с Софи и другими корреспондентами. Софи лишилась поддержки учёного в поисках доказательства теоремы Ферма и, к большому ее сожалению, была вынуждена заняться другими задачами. Метод Софи Жермен позднее использовали Лагранж и другие специалисты. Как бы то ни было, её вклад в доказательство теоремы оказался наиболее важным из всех сделанных в период с 1738 по 1840 год, когда были опубликованы труды Эрнста Куммера (1810–1893).

На протяжении почти 400 лет никто не мог ответить на вопрос, верна ли гипотеза Ферма? Является ли она теоремой — иными словами, существует ли ее доказательство? Более того, если это в самом деле теорема, то где ошибся Ферма в своём предполагаемом «чудесном доказательстве», так как он, несомненно, ошибся? Крайне маловероятно, что гипотезу, над которой столько лет бились лучшие умы человечества, доказал сам Ферма.

Многовековое ожидание завершилось в 1995 году усилиями Эндрю Уайлса, которому удалось найти доказательство лишь со второй попытки, спустя несколько лет работы, при этом он использовал сложнейшие и новейшие методы теории чисел. Вопреки ожиданиям, найденная им связь между модулярными формами и эллиптическими кривыми, которую он применил в доказательстве, отличалась новизной. Таким образом, теорема Ферма наконец была доказана.

Наибольшую славу Софи принесла тема колебаний тонких пластинок, находившаяся на стыке физики и математики. После того как она представила в Академии наук два доклада, её труд «О теории упругих поверхностей» наконец был удостоен премии (а также золотой медали весом в один килограмм) за полноту и глубину содержания. Однако Софи не явилась на церемонию вручения премии в знак несогласия с позицией некоторых академиков, в числе которых был Симеон Пуассон.

Заслуги Софи Жермен были оценены по достоинству, только когда она достигла зрелого возраста: Институт Франции удостоил её особой медали за научные труды, и она стала первой женщиной, посетившей заседание Академии наук, не будучи при этом женой академика. Софи пришла на заседание спустя семь лет после награждения. Ее вёл под руку великий Жозеф Фурье (1768–1830), секретарь Академии.

Софи Жермен занялась изучением упругости пластин, узнав о результатах экспериментов немецкого инженера и физика Эрнста Хладни (1756–1827) — любопытных фигурах Хладни. Фигуры Хладни, подобно цирковым фокусам, были продемонстрированы учёным из Института Франции и даже Наполеону. Эти неожиданные узоры образуются при вибрации покрытых песком стеклянных пластинок под действием скрипичного смычка. Многие из них отличаются красотой и симметрией. Фигуры Хладни стали первым известным проявлением физического явления, позднее названного двумерными гармоническими колебаниями.

Академия наук организовала открытый конкурс, целью которого было найти законы, описывающие колебания упругих пластинок. В 1813 году поданная на конкурс статья Софи Жермен «О колебаниях упругих пластинок» была удостоена первой премии. Для Софи, которую часто обвиняли в том, что ее доказательства содержат пробелы и неясные моменты, присуждение премии было равносильно ритуалу посвящения в учёные.

Последние работы Софи были посвящены дифференциальной геометрии, в частности кривизне поверхностей. В статье «О кривизне поверхностей» она впервые применила понятие средней кривизны, позднее ставшее классическим. Если c1 и с2 — наибольшая и наименьшая кривизна, то средняя кривизна, или кривизна Жермен, определяется по формуле:

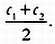
Софи возобновила переписку с необщительным Гауссом, и тот порекомендовал руководству своего Гёттингенского университета присвоить Жермен степень почётного доктора. Решение было принято лишь в 1830 году, а Софи умерла 27 июня 1831 года, так и не получив степень.

К несчастью, она умерла вовсе не той смертью, которую заслуживала: после двух лет страданий Софи скончалась от рака груди, который в то время считался неизлечимым. В свидетельстве о её смерти родом занятий значится «рантье». Жермен в самом деле была рантье, но куда лучше было бы написать «математик».

В мире науки Софи Жермен почитают за её талант, а для женщин всего мира она стала примером для подражания. В Париже именем Софи Жермен названа улица.

Упоминается эта женщина-математик и в научно-фантастических романах — ещё один шаг на пути к бессмертию. Имя Софи Жермен также носит и кратер на Венере. Однако высшей данью уважения её труду стали школы и институты, названные в её честь.