Основоположник геометрической теории чисел

Герман Минковский (Hermann Minkowski)родился 22 июня 1864 г. в Алексотах (пригороде Каунаса в сегодняшней Литве, в то время входивших в состав Ковенской губернии Российской империи), в купеческой семье немецких граждан еврейского происхождения.Уже его дед, Борух Яковлевич Минковский, был купцом первой гильдии в Вильне. На пожертвования его отца, купца первой гильдии Левина Боруховича Минковского, была построена Хоральная синагога в Ковно (1872). Мать, Рахиль Исааковна Тойбман, родом из Шакинова, была домохозяйкой; её родители впоследствии поселились в Мемеле (ныне Клайпеда) и таким образом вся семья получила прусское подданство. После рождения старшего сына Макса, Левин и Рахиль Минковские покинули Шакинов и поселились в Алексотах, где родились их второй сын Оскар (1858—1931), дочь Фанни (1863—1954) и Герман.

Детские годы Герман Минковский провёл в Ковно, здесь родился его младший брат Тувья (впоследствии Тоби, 1868—1906). В 1872 году, по окончании строительства синагоги, семья переехала в Кёнигсберг, где Левин Минковский занялся экспортом ковров.

Учился Герман в Альштадтской гимназии в Кёнигсберге. Его математические способности проявились ещё в школе. В одном классе, когда учитель не мог понять математической задачи, написанной на доске, ученики хором повторяли: "Минковский, помоги".

Восьмилетний курс гимназии Минковсний закончил за пять с половиной лет. В 1879 году Герман закончил гимназию. Далее он учился в университетах Кёнигсберга и Берлина. В общей сложности он учился пять семестров в Кёнигсберге, главным образом у Ф. фон Линдемана, В. Вебера и В. Фойгта, и три семестра в Берлине, где он слушал лекции Э. Куммера, Л. Кронекера, К. Вейерштрасса, Г. Гельмгольца и Г. Кирхгофа. Среди его друзей-студентов — Давид Гильберт.

Весной 1881 г. Парижская академия наук объявила конкурс на решение задачи о разложении целых чисел на пять квадратов. Минковсний, вопреки условиям конкурса, представил свою работу на немецком языке. Уже в этом возрасте он владел алгебраическими методами, в частности, теорией элементарных делителей, а также такими трансцендентными методами, как ряды Дирихле и суммы Гаусса. За эту работу, в заголовке которой стоял эпиграф: „Ничто не прекрасно кроме истины, одна истина прекрасна", Минковский получил большой приз Парижской академии. Когда присуждение этой премии Минковскому стало известно в Париже, шовинистическая пресса позволила себе ряд выпадов против автора. Однако французские академики К. Жордан и Ж. Бертран немедленно стали на сторону Минковского. „Работайте, пожалуйста, чтобы стать выдающимся математиком",— писал Жордан. Этот завет знаменитого французского математика Минковский выполнил.

В мемуаре, получившем премию, Минковский исследует разные нерешенные вопросы о квадратичных формах арифметическим методом, хотя сами эти вопросы и имеют иногда, собственно, геометрический смысл. К числу самых блестящих результатов относится следующий.Совокупность всех поворотов (без отражений и с отражениями), при помощи которых данная параллелепипедальная система точек может быть совмещена сама с собой, при условии, что одна её точка остается на месте, называется группой поворотов данной параллелепипедальной системы. Эти группы играют основную роль в кристаллографии. Их для трёхмерных решеток всего семь. Порядки этих семи групп суть 2, 4, 8, 12, 16, 24 и 48. Сколько может быть различных таких групп в случае n-мерной параллелепипедальной системы? Можно показать, что их ограниченное число. Но сколько их именно, и тем более, каковы их порядки, вообще говоря, можно узнать только подробно изучив решетки данного числа измерений. Поэтому особенно удивителен результат Минковского, по которому оказывается, что точное наименьшее кратное порядков всех таких групп для данного n может быть сразу выписано через число n.

Гильберт вспоминал, что Минковсний отказался от денежной премии в пользу бедного соученика и утаил это от своей семьи. Это лишь один пример его доброты и скромности, о которых знали все люди, соприкасавшиеся с ним.

В 1885 году Минковский получает докторскую степень. Диссертация относилась к теории квадратичных форм в пространстве произвольного числа переменных.

В 1887 г. в Бонне, где Минковсний был приват-доцентом, состоялась его встреча с Генрихом Герцем, который убеждал Минковского заняться физикой.

В 1893 г. он был назначен экстраординарным, а затем ординарным профессором Боннского университета. В 1895 году Минковский возвращается в Кёнигсберг, но вскоре переезжает в Цюрих (1896). В Цюрихе Минковский работал в политехникуме вместе с Д. Гурвицем. Его учеником был А.Эйнштейн, которого Минковсний особенно не выделял.

Первые результаты Минковского касались теории квадратичных форм. В 1896 году он представил знаменитую лемму, известную как «Теорема Минковского о выпуклом теле» — о том, что выпуклая область n-мерного пространства, объёмом

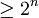
и симметричная относительно начала координат, непременно содержит точку с целочисленными координатами, отличную от начала координат. По словам Дж. Касселса, вся геометрия чисел основана на этой лемме. После создания геометрии чисел Минковский много и плодотворно работает над применением полученных результатов в других областях теории чисел: диофантовы приближения, теория многогранников и другие. Ему принадлежат фундаментальные достижения в геометрии выпуклых тел.

Всё в природе одновременно и непрерывно и дискретно. Дискретное в области чисел изучается теорией чисел. Все дискретное обладает структурой. Это является причиной того богатства и многообразия связей, которыми выделяется теория чисел среди других отделов математики. Дискретное и бесконечно повторяемое в геометрии хотя не раз и появлялось в разных математических исследованиях, но последовательно в математике до конца Х1Х столетия не изучалось. Минковский первый поставил себе целью разработать теорию чисел геометрическими методами.

Он явился создателем новой области математики, названной им геометрией чисел, соединяющей в себе изящество геометрии с глубиной теории чисел. Таким образом теперь прерывное в природе изучается всеми тремя основными методами математики: арифметическим, в элементарной теории чисел, аналитическим, в аналитической теории чисел, и геометрическим, в созданной Минковским, и одновременно с ним Г. Вороным, геометрической теории чисел.

Многие трудные вопросы теории чисел приобрели в руках Минковского при помощи этого метода необыкновенную прозрачность, естественность и изящество. Французский академик Ш. Эрмит, многие годы занимавшийся арифметическими исследованиями, был совершенно поражён. В ответ на письма, в которых Минковский сообщал ему свои результаты, Эрмит пишет: „С первого взгляда я понял, что Вы пошли гораздо дальше моих работ, открыв нам в арифметических исследованиях совершенно новые пути. Я преисполнен удивления и восхищения перед Вашими принципами и результатами, они открывают передо мной как бы совсем новый арифметический мир, в нём основные вопросы нашей науки рассматриваются с блестящим успехом, который должны будут признать все математики".

В 1897 году Минковский женился на Огюсте Адлер из Страсбурга. У них были две дочери: Лили родилась в 1898 г. и Рут родилась в 1902 г.

С 1902 года и до конца жизни Минковский работал в Гёттингенском университете, профессором математики, рядом с близким другом Д. Гильбертом. Одним из его студентов там был Константин Каратеодори.

Большая часть его работ посвящена теории чисел. Но он также внёс значительный вклад в геометрию, топологию, математическую физику, гидродинамику, теорию капиллярности.

Минковсний (вместе с Г.Ф. Вороным) является основоположником геометрической теории чисел. Основным объектом её изучения являются пространственные решётки - системы всех «целых» точек, т. е. точек, координаты которых в заданной прямолинейной системе координат (прямоугольной или косоугольной) выражаются целыми числами. С помощью геометрических решёток ему удалось доказать много теорем теории чисел. Пространственные решётки имеют большое значение в кристаллографии. Геометрические методы теории чисел он изложил вкнигах "Геометрии чисел" (1896) и "Диофантовы приближения" (1907).

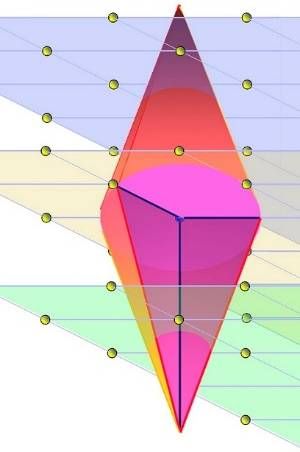
      Теоремой о многограннике Минковский стал в один ряд с О. Коши, давшим другой классический результат теории многогранников — единственность выпуклого многогранника, имеющего сетку данного топологического типа с данными гранями. Эти две теоремы, наряду с теоремой Л.Эйлера о соотношении между числами граней, ребер и вершин и теоремой Э. Штейница о реализуемости многогранника с любой заданной сеткой, являются четырьмя основными теоремами всей теории многогранников.

Когда появилась книга Минковского „Геометрия чисел" („Geometrie der Zahlen"), Эрмит выразил своё восхищение следующими словами: „Мне кажется, что я вижу обетованную землю". Действительно, исходя, главным образом, из одной весьма общей геометрической леммы, Минковский получает множество как старых, так и новых глубоких арифметических результатов. Теория алгебраических единиц, теорема о конечности числа классов целочисленных квадратичных форм с данным определителем, приближение к нескольким вещественным величинам при помощи дробей с одинаковыми знаменателями, теория непрерывных дробей и т. д., — вот вопросы, которые им разбираются при помощи геометрического метода.

Осуществленная им геометризация теории чисел определила новое направление математических исследований, связанное с гёттингенской математической школой, создателем которой Минковский являлся наряду с Давидом Гильбертом и Феликсом Клейном.

Полученные им в 1896 г. результаты положили начало важному разделу геометрии - теории выпуклых тел.

Особенно важна работа Минковского 1905 г., в которой он показывает, что способ приведения положительных квадратичных форм, предложенный Эрмитом, ведёт к области приведения, имеющей вид выпуклой пирамиды с ограниченным числом граней. Ещё начиная с 1883 г. Минковский не раз возвращается к способу приведения Эрмита, но только в работе 1905 г. ему удается, наконец, дать полное доказательство указанной основной, относящейся к этому способу, теоремы.

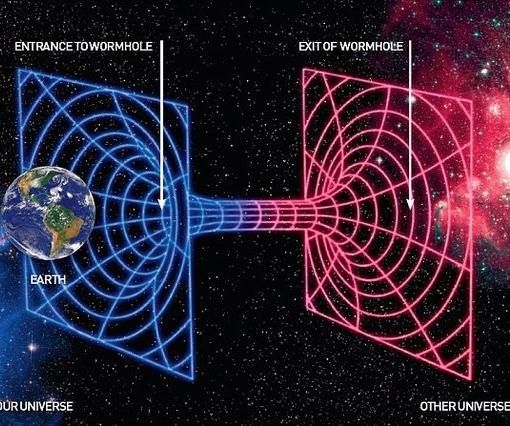
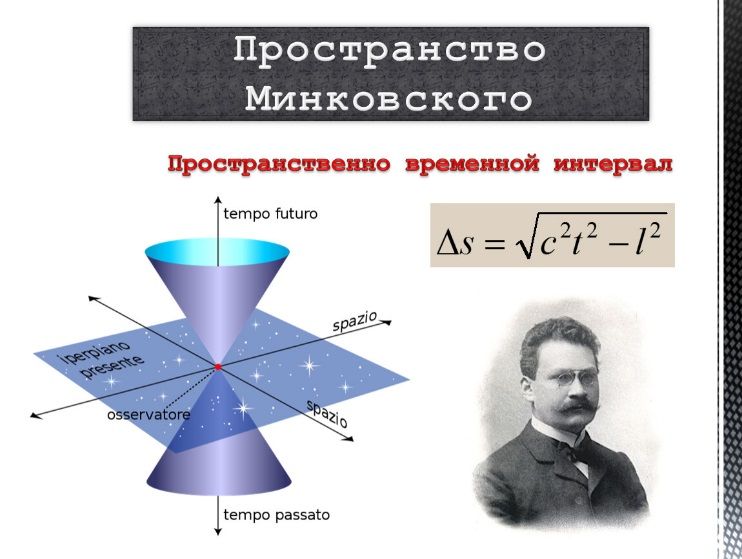
В 1907—1909 годах Минковский выступил с рядом статей и лекций, где предложил так называемую «геометродинамику» —четырёхмерную математическую модель кинематики теории относительности. В 1907 году он предположил, что специальная теория относительности, сформулированная Эйнштейном и основанная на более ранних работах Лоренца и Пуанкаре, лучше всего может быть описана в четырехмерном пространстве (известном сейчас как пространство Минковского), в котором время и пространство не разная суть, а являются измерениями пространства-времени, в которое хорошо вписывается геометрия Лоренца специальной теории относительности. Это предположение помогло Эйнштейну в формулировке общей теории относительности.

В 1908 появилась фундаментальная работа Минковского «Основы теории электромагнитных процессов в движущихся телах», в которой мировой постулат применяется для установления уравнений электромагнитного поля любой движущейся материи.

В 1908 году, незадолго до смерти, Минковсний прочитал в немецком научном обществе лекцию о мире, пространстве, времени, в которой произнёс знаменитую фразу: «Отныне и навсегда пространство и время превращаются лишь в тени, и только некий род единства того и другого сохраняет независимое существование».

Он высказал постулат о том, что все физические законы должны быть инвариантны относительно группы преобразований Лоренца и назвал его "мировым постулатом". В фундаментальной работе "Основы теории электромагнитных процессов в движущихся телах" (1908) мировой постулат применяется для установления уравнений электромагнитного поля любой движущейся материи.

В написанной в 1909 г. работе "Пространство и время" он дал геометрическую интерпретацию кинематики и ввёл четырёхмерное пространство с гиперболической метрикой. Альберт Эйнштейн исключительно высоко ценил вклад Минковского в развитие релятивистской теории.

М. Борн вспоминал: «На второй год моего пребывания в Гёттингене я стал личным ассистентом Гильберта. Каждое утро я должен был находиться у него, чтобы обсуждать предстоящие лекции и семинарские занятия. Часто приходил и Минковсний, он принимал участие в наших разговорах или возбуждал новые вопросы. Для меня это было чудесное время учёбы не только в области науки, но и в делах человеческой жизни. Я уважал и любил их обоих, и они никогда не давали мне почувствовать, сколь велика разница в званиях и жизненном опыте между ними и мной; напротив, они обращались со мной, как с более молодым коллегой. Когда Минковсний возвращался домой, он брал меня в качестве попутчика, и начинал какой-нибудь разговор по существу нашей науки или о товарищах по специальности, с которыми он непосредственно переписывался, или о философских, социальных, политических вопросах. Иногда мы прогуливались довольно долго, прежде чем вернуться домой ...

Я ещё совсем мало прожил в Гёттингене, когда был приглашён Минковским на обед. Так я впервые лично познакомился с ним, увидел его прекрасное широкое лицо, его тёмные выразительные глаза и услышал его низкий, немного грубоватый голос. Меня представили его жене и двум маленьким дочерям. Кроме меня, был там ещё только один гость, Константин Каратеодори, молодой грек, который раньше служил в Греции инженером, работал в Египте и Месопотамии, а затем посвятил себя чистой математике и теперь был приват-доцентом в Гёттингене. Мы вскоре стали близкими друзьями. Он был замечательным математиком и умер в Мюнхене несколько лет назад, будучи уже профессором ...

Минковский не был блестящим преподавателем, но он увлекал простотой и ясностью своего изложения, часто оживляемого остроумными замечаниями. Создавалось впечатление, что то, о чём он рассказывал, было только что создано им в процессе изложения. Во многих случаях так оно и было. Это я могу показать, сославшись на случай, который произошёл на лекции по «Analisis situs», как тогда называлась область, именуемая ныне топологией ... Минковский начал с того, что он хотел бы пояснить нам на основе понятия этой дисциплины, на примере так называемой проблемы четырёх цветов. При изготовлении географических карт выяснилось, что для закраски любой карты так, чтобы две соседние страны были различны по цвету, необходимо и вполне достаточно иметь четыре цвета. Он добавил: «К сожалению, этого не удалось доказать. Но этим занимались только математики третьего ранга. Я надеюсь это доказательство получить». И здесь он начал свои дедукции. Прошло две - три недели, дело всё осложнялось; и даже через три - четыре недели решения не было видно. Когда мы однажды утром собрались в аудитории, разразилась сильная гроза, сверкали молнии, лил дождь. В тот момент, когда Минковский входил в аудиторию, последовал страшный удар грома. Минковский спокойно прошёл к кафедре и сказал совершенно серьёзно: «Небо гневается на мою дерзость. Моё доказательство проблемы четырёх цветов тоже неверно». Затем по его лицу пробежала улыбка, и он приступил к чтению лекции ... По вечерам я часто бывал гостем у Минковских и узнал его как любезного хозяина, который вступал в беседы на любые темы и везде находил сказать что-нибудь существенное. Всегда у него под рукой была меткая цитата, часто из «Фауста» Гёте, которого он знал наизусть...Госпожа Минковская доверила мне (после смерти Минковского), по предложению Гильберта, просмотр оставленных им физических записей, а математические записи передала Андрею Шпайзеру. Мне удалось построить из кратких заметок, по крайней мере, одну работу и опубликовать её».

10 января 1909 г. за обедом Минковсний внезапно почувствовал сильный приступ аппендицита. Ночью была проведена трудная операция, но состояние больного всё ухудшалось. 12 января 1909 года Г. Минковсний умер. Ему было всего 44 года.Его смерть стала страшным ударом для всей новой гёттингенской школы математики. Для Гильберта потеря друга обернулась незаживающей раной, от которой он страдал до глубокой старости.

        С именем Г. Минковского связаны термины:Гипотеза Минковского, Диаграмма Минковского, Задача Минковского, Кривая Минковского, Неравенство Брунна — Минковского, Неравенство Минковского, Пространство Минковского в специальной теории относительности, Пространство Минковского (метрическая геометрия), Размерность Минковского, Расстояние Минковского, Сумма Минковского, Теорема Минковского о выпуклом теле, Теорема Минковского о многогранниках, Функционал Минковского, Функция Минковского.

Д.Гильберт издал в 1911 году полное собрание трудов своего друга. В честь учёного названы кратер Minkowski на Луне и астероид 12493 (Minkowski).

Рассказывают, что …

•    Прадед отца — еврейский учёный-энциклопедист Борух бен Яаков Шкловер, получил в 1764 году звание раввина в Бресте и служил даяном (титул иудейского религиозного судьи) в Минске, изучал медицину в Великобритании и на иврите опубликовал труд по тригонометрии (1784), а также сочинения по астрономии, анатомии и гигиене, перевёл на иврит труды Евклида; последние годы жизни провёл в Слуцке, где служил даяном и придворным врачом князя Радзивилла. Его внук, Карлинский ребе и комментатор Талмуда Ицхок бен Аарон (1788−1851), принял фамилию Минковский.
  

• У Германа было два старших брата: Макс, унаследовавший компанию отца, занимавшийся зерноторговлей и служивший консулом Франции, и Оскар – учёный-медик, описавший синдром Минковского — Шоффара и занимавшийся изучением патофизиологии сахарного диабета.

• В Гёттинген профессор Минковский попал необычным образом. Главную роль в этом сыграл Феликс Клейн, формировавший физико-математическую школу Гёттингена и сделавший его мировым центром физико-математических исследований.

       Когда в 1902 году пришло предложение Гильберту из Берлина, руководство Гёттингенского университета по-настоящему почувствовало угрозу потерять математическую звезду первой величины. До сих пор никто не отказывался от должности в столичном университете, по-прежнему остававшемся наиболее привлекательным и престижным для ученого любого ранга.

Чтобы побудить Гильберта остаться в Гёттингене, в университете было создано ещё одно место ординарного профессора и его предоставили Герману Минковскому, многолетнему другу и соратнику Гильберта. Минковский переехал в Гёттинген, а Гильберт отказался от предложения из Берлина. С назначением Минковского нарушалась старая традиция немецких университетов строго ограничивать количество преподавателей-евреев в каждой отдельно взятой области науки.

*Концепция пространства-времени сыграла исторически ключевую роль в создании геометрической теории гравитации. В рамках общей теории относительности гравитационное поле сводится к проявлениям геометрии четырехмерного пространства-времени, которое в этой теории не является плоским (гравитационный потенциал в ней отождествлен с метрикой пространства-времени).

• Количество измерений, необходимых для описания Вселенной, окончательно не определено. Теория струн (суперструн), например, требовала наличия 10 (считая время), а теперь даже 11 измерений (в рамках М-теории). Предполагается, что дополнительные (ненаблюдаемые) 6 или 7 измерений свёрнуты (компактифицированы) до планковских размеров, так что экспериментально они пока не могут быть обнаружены. Ожидается, тем не менее, что эти измерения каким-то образом проявляют себя в макроскопическом масштабе.

В самом старом — бозонном — варианте теория струн требует 26-мерного объемлющего пространства-времени; предполагается, что "лишние" измерения этой теории также должны или могут быть компактифицированы сперва до 10, сводясь таким образом к теории суперструн, а потом уже до 4 обычных измерений.

• Минковский Оскар - физиолог, патолог, клиницист, доктор медицины, брат Германа Минковского. Оскар родился в Алексотах (пригороде Каунаса в сегодняшней Литве).

После окончания гимназии в Кёнигсберге изучал медицину в университетах Страсбурга, Фрайбурга, Кёнигсберга (1881). В 1900–1905 главный врач городской больницы и одновременно (с 1904) профессор Академии практической медицины в Кёльне.

Исследования Оскара посвящены проблемам сахарного диабета, а также обмену веществ, желтухе, подагре и другим. В 1923 вместе с группой немецких врачей консультировал В.Ленина. Умер Оскар Минковский 18 июля 1931 в Фюрстенберг-на-Хафеле, Германия.

• То, что открыл и внёс в физику Альберт Эйнштейн, – поистине революционно, и одним из первых, кто понял это, стал выдающийся немецкий физик Макс Планк (1858–1947), который написал:«Эйнштейновская концепция времени превосходит по смелости все, что до этого времени было создано в умозрительном естествознании и даже в философской теории познания».

В 1908 году Герман Минковский, учивший Эйнштейна в Цюрихском политехническом институте, создал для его специальной теории относительности математический аппарат. Модель Минковского очень помогла Эйнштейну в разработке его общей теории относительности.

• Вначале Эйнштейн счёл запись уравнений теории относительности в тензорной форме "излишней учёностью" и шутил, что "с тех пор как теорией относительности занялись математики, он и сам перестал её понимать", но уже к 1914 г. он освоил тензорный анализ, а в 1916 г. признал, что Минковский этим облегчил ему переход от СТО к ОТО. Но ещё в 1911 г он разглядел в 4-мерном мире Минковского самое главное для себя – то, что в этом мире "пространственно-временные соотношения между физическими событиями изображаются геометрическими теоремами" . Так началась эйнштейновская геометризация физики.

• Геометрия мира Минковского остается для неспециалистов труднодоступной абстракцией. Между тем к математическим знаниям, даваемым теперь средней школой, надо добавить не много, чтобы развить представление о псевдоевклидовом пространстве. Прежде всего, требуется понятие абстрактного линейного пространства и его разновидности – евклидова пространства, умение различать линейные и метрические свойства пространства. Эти понятия являются исходными для построения геометрической теории. Без достаточно свободного владения ими и связанным с ними алгебраическим аппаратом нельзя преодолеть привязанность к привычной наглядности образов и проникнуть в мир форм, скрытых от непосредственного зрительного восприятия.

Геометрия пространства Минковского позволяет наглядно интерпретировать кинематические эффекты специальной теории относительности (изменения длин и скорости течения времени при переходе от одной инерциальной системы отсчета к другой) и лежит в основе современного математического аппарата теории относительности.

• «Тот ещё лентяй!» – сказал как-то Герман Минковский о своём ученике Альберте Эйнштейне. Последний, впрочем, никогда этого не отрицал. Вспоминая о годах учебы в Цюрихском университете, сейчас это Швейцарская высшая техническая школа, он признавал: «В студенческие годы я плохо понимал, что куда более основательное понимание базовых принципов физики напрямую связано с самыми изощренными методами в математике».

Минковский как раз преподавал математику и геометрию – и ему стоило больших трудов заманить одаренного студента в свою аудиторию: Эйнштейн вёл в Цюрихе «исключительно богемный» образ жизни и не интересовался ничем, кроме полюбившейся ему физики. Но даже когда они оба почти одновременно опубликовали работы о пространстве и времени, ставшие основой теории относительности, Минковский не покушался на авторитет своего ученика: забыл его университетские прогулы и восхвалял на всех ученых собраниях.

• Синагога в Каунасе, построенная на деньги Левина Минковского, существует и сегодня – несмотря на повреждения от снарядов Второй мировой войны и расистский инцидент 2011 года, когда неизвестные оклеили стены плакатами с призывами к евреям «убираться вон».