Один из первых крупнейших математиков России

Виктор Яковлевич Буняковский родился 16 декабря 1804 г. в городе Баре Могилевского уезда Подольской губернии в семье подполковника конно-польского полка. После гибели отца в 1809 году в Финляндии Виктор воспитывался в семье его сослуживца генерала А.П. Тормасова и получил здесь начальное образование.

      В 1820 г. Буняковский (вместе с сыном Тормасова) уезжает для завершения образования за границу и около семи лет живёт в Кобурге (Германия), в Лозанне и Париже. В Париже он слушал лекции по математике и механике в Сорбонне и в Коллеж де Франс. Его учителями были П.С.Лаплас, С.Д.Пуассон, Ж.Фурье, О.Коши, А.Лежандр, А.Ампер. Буняковский становится сторонником взглядов О.Коши. Он перевёл на русский язык сочинение Коши по анализу, снабдив его ценными комментариями. По этой книге училось целое поколение математиков.

В 1825 году Буняковский получает в Париже степень доктора. Его диссертация состояла из двух работ: "О распространении теплоты внутри твердого тела" и "О вращательном движении в сопротивляющейся среде плоской системы, имеющей постоянную толщину и определенный контур".

          В 1826 году Буняковский возвращается в Петербург и приступает к педагогической, научной и организаторской деятельности в Первом кадетском корпусе (1827 г.), Морском корпусе (1827-1862 гг.), Горном институте и Институте корпуса инженеров путей сообщения (1830-1846 гг.), был профессором Петербургского университета (1846-1889 гг.). С 1858 г. работал главным экспертом правительства по вопросам статистики и страхования. С 1864 г. на протяжении 25 лет являлся вице-президентом Академии наук. Он написал несколько учебников, в том числе «Арифметику» (1844 г.), принятую за образец, был редактором математического отдела «Энциклопедического словаря» (1861-1863 гг.), сотрудничал в «Энциклопедическом словаре» А.А. Плюшара (1830-е гг.). В работе "Арифметические исследования " (1830) доказана теорема, выражающаяся формулой:

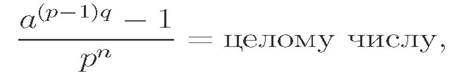
где р - простое число, а и n - любые целые числа, а не делится на р, q = рn-1.

    Там же Буняковский дал новый и простой вывод формулы для решения линейного уравнения с двумя неизвестными.

         В 1846 г. его избирают профессором Петербургского университета.

Приход в университет Буняковского, а позже и Сомова О.И., Чебышева П.Л, выдвинул университет на одно из первых мест в мире.

В университете Буняковский читал курсы аналитический механики, следуя Пуассону и Остроградскому, дифференциального и интегрального исчислений, следуя Коши, теории вероятностей, следуя собственному сочинению. Круг его научных интересов был широким.

Лекции Буняковского отличались отчётливостью и изяществом с изумительной ясностью, что привлекало внимание слушателей. Студенты и коллеги ценили в нём не только учёного и первоклассного лектора, но и очень хорошего, отзывчивого и душевного человека, готового всегда словом и делом помочь начинающему учёному.

В связи с ухудшением здоровья, в 1859 г. Буняковский оставил университет. В знак признания его заслуг университет избрал его своим почётным членом.

В 24 года Буняковский был избран адъюнктом Петербургской Академии наук. В 1841 г. его избирают ординарным академиком. В течение 25 лет (с 1864 г) он был вице-президентом Академии наук.

В. Буняковский вместе с М. Остроградским входил в состав комиссии по изданию трудов Л. Эйлера. Особенно его интересовали работы по теории чисел. Буняковский решил собрать эти работы и издать их отдельно. При участии молодого П. Чебышева ему в 1849 г. удалось это осуществить.

Буняковский и сам внёс существенный вклад в теорию чисел (решение неопределенных уравнений, новое доказательство квадратичного закона взаимности, теория числовых функций). Ни один солидный курс теории чисел в наше время не может не упомянуть о его работах.

        Суммирование конечных рядов В.Я. Буняковский основывает на тождестве

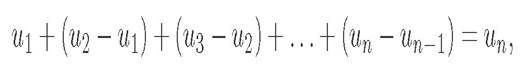
все члены которого считаются положительными:

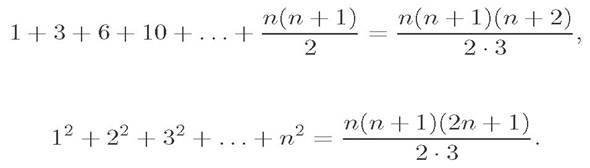
        Большой вклад он внёс в теорию вероятностей. В 1846 году появился труд Буняковского, послуживший началом его всемирной известности, – «Основания математической теории вероятностей». Этот обширный трактат, кроме теории, заключал в себя и историю возникновения и развития теория вероятностей; в нём впервые сведено вместе всё то, что было выработано по этой теории трудами известных математиков, начиная с Паскаля и Ферма, даны объяснения относительно новых решений самых трудных и запутанных вопросов, указано много практических приложений теории вероятностей, например, к вопросу о средней продолжительности жизни людей различных возрастов, к определению достоверности свидетельств и преданий, к вспомогательным кассам и страховым учреждениям, к определению погрешностей при наблюдениях, к вопросам судебного дела, к вычислению вероятностных потерь в войске. Форма «Оснований математической теории вероятностей» отличались такой удобопонятностью и изяществом, что немецкий математик Гаусс и французский химик Бьенеме учились русскому языку по этому сочинению.

Работы Буняковского были продолжены П. Чебышевым, А. Марковым, А.Ляпуновым. Буняковский интересовался приложениями теории вероятностей, он являлся постоянным экспертом правительства в вопросах статистики и страхования.

Среди работ по математическому анализу наибольшей известностью пользуется мемуар Буняковского "О некоторых неравенствах, относящихся к определенным интегралам или интегралам в конечных разностях" (1859 г). В нём он впервые установил замечательное неравенство, которое затем независимо от него было открыто Г.А. Шварцем (неравенство Буняковского – Шварца, хотя Г. А. Шварц нашёл это неравенство только в 1875 г., т.е. на 16 лет позднее). В функциональном анализе это неравенство является одним из основных положений.

Буняковский первый доказал важное неравенство математического анализа, утверждающее, что

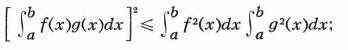
Это соотношение весьма часто употребляется в интегральном исчислении и в исследованиях, посвящённых вопросу о разложении произвольных функций по функциям ортогональной системы.

В геометрии Буняковский занимался вопросом доказательства V постулата Евклида, но, как и М. Остроградский, не сумел понять идей Н.И. Лобачевского и выступил против неевклидовой геометрии. В. Буняковский частично осуществил издание (1839 г.) "Лексикона чистой и прикладной математики", в котором даны объяснения математических терминов (от А до Д) и содержатся интересные материалы по истории математики.

Список его сочинений содержит 168 названий. Буняковский сыграл значительную роль в повышении научного уровня преподавания математики. Им были написаны учебники по арифметике для средней школы (1844 и 1849 г.г.), учебные руководства для военно-учебных заведений и гимназий.

    На протяжении всей жизни он интересовался конструированием различных измерительных и счётных приборов. В.Я. Буняковский изобрел планиметр, пантограф, прибор для суммирования квадратов и особый счётный прибор, названный им "самосчётами". Самосчеты использовались В.Я. Буняковским для вычисления средних месячных и годовых температур и высот барометра. Это был единственный прибор, облегчавший утомительные вычисления в метеорологии. Он оказал серьёзное влияние на развитие отечественной изобретательской деятельности, в частности на работы П.Л. Чебышева в области счётной техники.

В.Я.Буняковский не унаследовал от отца родовых имений и жил со своей большой семьей – женой Екатериной Николаевной и детьми (у него было три сына и три дочери) в Петербурге в казенной академической квартире. Его близкими друзьями были М.В.Остроградский, П.Л.Чебышев, О.И.Сомов, Э. Ленц. В жизни В. Буняковский был поразительно скромным и доброжелательным человеком.

Буняковский любил поэзию и в молодости сам писал стихи. Им были сделаны переводы "Чайльд-Гарольда" Байрона.

В 1875 г. было широко отмечено 50-летие научной деятельности Буняковского. Свои приветствия ему прислали все университеты, (он был почётным членом всех русских университетов) многие военные учебные заведения России, математические общества Москвы, Харькова, Казани. По этому случаю, Академия выбила медаль. На собранные по подписке средства Академия создала фонд для выдачи премии имени В.Я. Буняковского за лучшие работы по математике. Научная работа Буняковского протекала главным образом в Академии наук.

          Из 168 научных трудов около половины относится к теории чисел и теории вероятностей с её приложениями, а остальные - к вопросам анализа, геометрии и алгебры. Буняковский интересовался также практикой вычислений, предложил усовершенствованный вариант русских счётов. Ряд статей Буняковского посвящен статистике народонаселения, подсчёту вероятных контингентов русской армии, решению задач судопроизводства, определению погрешности наблюдений и т. д. Все эти работы содействовали успешному развитию теории вероятностей в России. Работы по теории чисел о сравнениях, квадратичном законе взаимности и другие возродили в русской науке интерес к теории чисел, успешно разрабатывавшейся в Петербургской Академии Наук в XVIII в. Работы Буняковского по геометрии относятся преимущественно к теории параллельных линий.

До глубокой старости Буняковский участвовал в деятельности Академии.

Лишь за несколько месяцев до смерти, почувствовав слабость, он отказался от должности вице - президента Академии. Его избрали почётным вице - президентом.

         Умер В.Я. Буняковский 12 декабря 1889 года. Он похоронен вместе со своей женой около церкви Смоленской Божией Матери, с северо-восточной стороны.

       В последний путь, на смоленское кладбище в Петербурге, покойного провожала большая часть членов Академии наук, в том числе П.Л.Чебышев и много других лиц. В отчёте Академии наук за 1890 г. относительно смерти Буняковского сказано: «Спокойна и тиха была его кончина, как спокойна и тиха была его долгая жизнь. Годы подкрадывались к нему незаметно, почти не давая себя знать на его душевных способностях, так что все мы, видя его перед нами в течение длинного ряда лет всегда одинаково бодрым и умственно здоровым, могли подчас забывать, что человек смертен». Наследники Буняковского после его смерти заявили о своём желании пожертвовать Санкт-Петербургскому университету часть библиотеки академика, состоявшей из математических книг.

Он был одним из первых крупных математиков России XIX века. Научные заслуги Буняковского были оценены по заслугам уже современниками. Он был почётным членом всех русских университетов, многих иностранных и русских учебных обществ. При Академии наук была учреждена премия его имени за лучшие сочинения по математике. Буняковский пользовался заслуженным авторитетом среди европейских учёных.

Рассказывают, что…

• Не будет преувеличением сказать, что Буняковский является отцом русской теории вероятностей, так как его "Основания “были первым полным сочинением по теории вероятностей на русcкoм языке.

      Автор и соавтор пособий по теоретич. и демографич. Статистике П.П. Шушерин

• Ещё совсем молодой гимназист Андрей Марков написал письмо Виктору Яковлевичу Буняковскому. На это письмо академик В.Я. Буняковский написал ответное, где в уравнениях, исследованных и решённых им, были показаны ошибки. В этом письме В.Я. Буняковский похвалил будущего известного академика и щахматиста А.А. Маркова (1856-1922) и отметил очень высокий для такого возраста уровень знания математики.

• Как профессор и человек Буняковский был «баснословно скромен». Вот что говорит об этой отличительной черте характера Буняковского один из его учеников В.А.Панаев: «Когда мы, по выслушании его (Буняковского) курса, экзаменовались у Остроградского, то нередко случалось, что иной воспитанник, получив дурной балл, обращался с жалобой к Буняковскому, утверждая, что он отвечал так, как было им Буняковским читано, а между тем получил у Остроградского дурной балл. Будучи сам огромной величиной в науке, Буняковский, не менее того, никогда сам не отказывался идти по этому случаю объяснится с Остроградским, и эти объяснения происходили в нашем присутствии. Искренно признавая за Остроградским гениальность, Буняковский, большей частью, начинал объяснение следующим образом: «Профессор, я преподавал своим слушателям тот или другой вопрос так, как он теперь стоит в науке, но, может быть, вы двинули вопрос вперёд, и мне это ещё неизвестно. Вот г-н № сказал мне, что он отвечал Вам так, как было мною изложено, а между тем получил дурной балл».
  

Обыкновенно было в этом случае, что Остроградский захохочет и скажет: «Пожалуйте, профессор, он Вам наврал, я знаю Ваш курс, г-н № говорил, ничего не понимая, чушь, а потому и получил дурной балл; проверьте сами!».

•  Характеризуя Буняковского как наставника и профессора, Н.Н. Божерянов говорил: «Виктор Яковлевич в классах и на экзаменах никогда и ни на кого, как говорится, не нападал, а между тем не отвечать из его предмета было всякому и стыдно, и страшно. Виктор Яковлевич никогда и нигде в конференциях и советах не порывался говорить и спорить громче других, а между тем везде и всегда его внимательно слушали и жаждали слушать, и слова его едва ли не были законом. Виктор Яковлевич никогда не высказывал честолюбия и претензий на награды, а между тем и честь, и слава, и награда – сами стучались к нему и в дверь, и в окна».
  

• По словам академика К.С. Веселовского, Буняковский «столь же крепко держался раз принятого порядка своего домашнего быта, как и другие любят перемены в жизни. Одною из таких привычек была для него умственная работа; он жил, когда работал, и жил только, чтобы работать, и его биография почти вся укладывается в рамки его библиографии».

• С М.В. Остроградским Буняковский познакомился впервые в Париже. Более близкое их знакомство произошло в конце 20-х годов девятнадцатого века в стенах морского корпуса, в котором они преподавали математические науки.
  

        Вот как описывает это знакомство их ученик С.И. Зелёный: «Вскоре после того, как виновник настоящего нашего собрания (Буняковский В.Я.) начал бороться с нашею математической неразвитостью, явился на то же поприще другой деятель; то был гениальный М.В. Остроградский. Я живо помню, как убелённый сединами и уже знаменитый наш первый кругосветный мореплаватель (адмирал И.Ф. Крузенштерн) ввёл в класс к Виктору Яковлевичу молодого тогда учёного; как дружески будущие корифеи науки протянули друг другу руки, как бы условливаясь действовать заодно на предстоящем им поприще». Об Остроградском Буняковский всегда отзывался с уважением и особенно ценил его заслуги в науке.

• При богатстве и глубине содержания, лекции Буняковского всегда отличались поразительной ясностью, увлекательностью и в то же время литературной красотой изложения, делали легко доступными самые сложные математические положения и увлекали даже безучастных слушателей. По отношениям к лекциям Буняковский проявлял замечательную аккуратность и в течение всего времени своей службы в университете не пропустил ни одой лекции и не опоздал ни разу.