Математика после уроков Задание №4
Решения задач задания № 3:
Если число a1b1c1 отлично от нуля, то оно обладает следующими свойствами:
b1 = 9;
a1b1c1 делится на 9.
Поэтому a1b1c1 – одно из чисел 99, 198, 297, 396, 495, 594, 693, 792, 891, 990. Остаётся заметить, что 594 → 99 → 891 → 693 → 297 → 495.
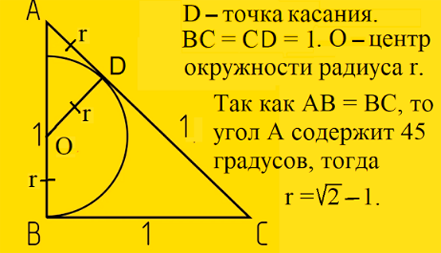
- По условию в комнате находятся пяти- и шестиногие существа, у которых в сумме 39 ног. Число ног у пятиногих оканчивается на 0 или 5. Но на 0 это число оканчиваться не может: тогда число ног у шестиногих будет кончаться на 9. В таком случае пятиногих может быть 1, 3, 5 или 7. Перебором определяем, что пятиногих существ – 3, а шестиногих – 4. То есть в комнате 4 стула
и 3 табуретки.
- Пусть x = 11n + r, где n ≥ 0, 0 ≤ r ≤ 10. Тогда [x/11] = n, n + 1 = [x/10] =
= n + [n+r/10], то есть 10 ≤ n + r < 20, 10 – r ≤ n ≤ 19 – r. Для каждого r от 0 до 10 получаем 10 решений.
Ответ: 110 решений.
- Пусть D=b^2–4ac=23, тогда b^2–23=4ac, b^2–25=4ac–2, (b–5)(b+5)= 2(2ac–1), следовательно b^2–25 делится на 4 (так как числа b–5 и b+5 имеют одинаковую чётность), но число 2(2ac–1) не делится на 4.
Новое задание:
- Функция f(x) определена для всех x, кроме 1, и удовлетворяет равенству:
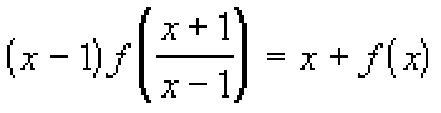
Найдите f(–1).
Решите неравенство: [x]•{x} <x – 1.
Существуют ли такие иррациональные числа a и b, что степень ab - число рациональное?
Подсказка. В качестве a можно взять корень из натурального числа.
От редакции: Редакция газеты «Обзор», предлагая своим читателям данные «уроки математики», хотела бы помочь нынешним старшеклассникам в большей степени освоить эту область знаний. Тем более что в последние годы министерство образования неоднократно указывало на то, что школьники в Литве знают математику, мягко говоря, неважно.
Но насколько предлагаемый ныне газетой математический курс всё же интересен сегодняшним старшеклассникам или хотя бы их учителям?
Какой вариант более востребован – бумажный или всё же тот, что по воскресеньям, после выхода очередного номера газеты, публикуется на сайте www.obzor.lt?
Что пригодилось вам, а что нет?
Свои комментарии и предложения вы можете отправлять в редакцию в любом удобном для вас виде: по электронной почте info@obzor.lt, как комментарий под публикациями на сайте или по телефону (+370 5) 275 31 53.
