Математика после уроков

Задание №3

Решения задач прошлого номера:

1. Единственного правильного ответа на эту математическую задачу нет, но есть несколько: на числа от 2 до 18 делятся 4876391520, 2438195760, 4753869120, 3785942160.

2. Задача решается несколькими способами, вот некоторые из них:

(99-9) : 9 + (99 – 9) = 100

(99 – 99) * 999 = 10*0

999 / 9 – 99 / 9 =100

(9 * 9 + 9) / 9 + 99 – 9=100.

3. Необходимо расставить знаки следующим образом - 6 / ( 1 – ( 3 / 4 ) ) = 24.

4. Пусть x > y, тогда (x+y)+(x–y)+xy+x/y =243, x(2y+y^2+1)=243y,

x=243/(y+1)^2, следовательно 3^5 делится на (y+1)^2. Тогда: a) y+1=1, т.е. y=0, что невозможно; б) y+1=3, y=2, x=54; в) y+1=3^2, y=8, x=24.

5. Пусть x – число дней, когда дежурили 9 богатырей, а y – дней, когда дежурили 10 богатырей, причём каждый из них дежурил z раз, тогда 9x + 10y = 33z. При z =1 решения нет. При z=2 имеем x=4, y=3.

Новое задание:

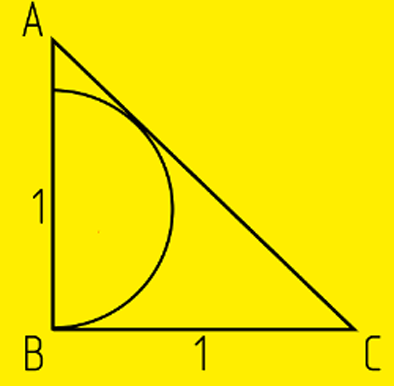
1. В треугольнике ABC угол B прямой, AB = BC = 1. Полуокружность с центром, лежащем на AB, касается AC. Найдите площадь полукруга.

2. Имеется трёхзначное число abc, берём cba и вычтем из большего меньшее. Получим число a1b1c1, сделаем с ним то же самое и т.д.

Доказать, что на каком-то шаге мы получим или число 495, или 0. Случай a1 = 0 допускается.

3. В комнате стоят трёхногие табуретки и четвероногие стулья. Когда на все эти сидячие места уселись люди, в комнате оказалось 39 ног.

Сколько в комнате табуреток?

4. Сколько решений в натуральных числах имеет уравнение [x/10] = [x/11] + 1?

5. Пусть a, b, c – целые числа. Может ли уравнение аx^2+bx+c = 0 иметь дискриминант, равный 23?