Математика после уроков. Задание №10

Решения задач прошлого задания:
- Если периметр прямоугольника равен 1996, то сумма длин его соседних сторон равна 998. Значит, длина меньшей стороны может принимать значения от 1 до 499. Если периметр прямоугольника равен 1998, то сумма длин его соседних сторон равна 999, а длина меньшей стороны может принимать те же значения: от 1 до 499. То есть в обоих случаях прямоугольников поровну, а именно, 499.
Ответ: Поровну.
- Меридианы делят глобус на 24 части (дольки), а параллели делят каждую дольку на 17 + 1 = 18 частей. Всего 18•24 = 432 части.
Ответ: На 432 части.
3. Ответ: 9•55 чисел.
4. Ответ: 3 ожерелья.
- Пусть M = 100a + 10b + c– искомое трёхзначное число. Для определения его цифр согласно условию задачи составляем уравнение M = a! + b! + c! (1). Из анализа правой и левой частей этого уравнения с учётом равенств 4!=24, 5!=120, 6!=720, 7!=5040 заключаем, что ни одна цифра числа M не превосходит 6. Поэтому число M не превосходит 666, откуда следует, что ни одна цифра числа M не превосходит 5. Согласно равенству (1) число должно быть трёхзначным, поэтому по крайней мере одна из цифр этого числа равна 5, ибо в противном случае это число окажется двухзначным. Таким образом,
M ≤ 3∙5!=360, следовательно a≤3. Легко проверить, что в случаях a=2 или a=3 уравнение (1) не выполняется, следовательно a=1. В этом случае b=5 не подходит, следовательно c=5. Для нахождения c рассматриваем уравнение
1b5=121+b!, которое имеет решение b=4.
Ответ: 145.
Новое задание:
Пара натуральных чисел (а, b) удовлетворяет уравнению ab + а + b = 2020. Найдите все возможные значения суммы a+b.
Найдите количество восьмизначных чисел, произведение цифр каждого из которых равно 3375.
Решите неравенство
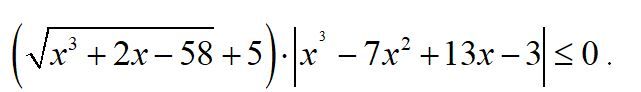
специально для «Обзора»
0
Опубликовано 17 января в 08:00
